Frequency
is the number of complete vibrations occurring in one second \[f\]

periodic time
It is the time required to complete a complete movement. \[T\]
In this experiment we will study the harmonic motion of a body
and determine the restoring force, displacement, kinetic energy and potential energy of a body vibrating about the equilibrium position.


Hooke's law
Hooke's law is the law of elasticity discovered by the English scientist Robert Hooke in 1660 AD,
which states that when relatively small deformations occur to a body,
the amount of displacement or size of the deformation is directly proportional to the force of the deformation or compression,
and on the other hand, under these conditions,
the body returns to its original shape and size when the force acting on it disappears. The elastic behavior of solid materials can be explained according to Hooke's law; the deformation that occurs to the molecules of these materials composed of atoms or ions is directly proportional to the force causing this displacement,
and its opposite in direction.
Hooke's law is expressed mathematically by the relationship,
F = - kx


pendulum

Simple pendulum: It is a weight suspended at the end of a weightless, non-extensible string. The other end of the string is fixed

return force \[F= - mg .sin (𝜃)\] The return force is negative because the component of the force is always in the opposite direction to the displacement.

We consider the motion of a pendulum to be simple harmonic motion if the pendulum is displaced by an angle of less than 15 degrees.

n this simulation we will study the factors affecting theperiodic time of a pendulum in simple harmonic motion.

\[T = 2𝜋\sqrt{\frac{L}{g}}\]

mechanical waves

The wave It is a disturbance that transfers energy through matter or space without any transfer of matter particles.

a medium:The material through which the wave travels

Mechanical waves: A wave that requires a material medium to travel through. Example - Sound waves. Sound waves cannot travel through a vacuum. .

When a mechanical wave moves through a physical medium, the particles in the medium oscillate with simple harmonic motion.


simple harmonic motion

The blue ball above is in simple harmonic motion. Imagine that this ball represents a particle in a solid. If this particle is bound to other particles near it, its motion will affect the motion of the particles around it..

transverse wave

While the wave itself travels from left to right (horizontally). This particular type of wave motion is called a transverse wave.
Transverse Wave- A wave in which the particles of the medium move perpendicular to the direction of the wave motion.

Longitudinal Wave

Wave can also move through a material when the particles of the medium vibrate back and forth in the direction of the wave motion. This type of wave is called a longitudinal wave. - A wave in which the particles of the medium move parallel to the direction of the wave motion.
Longitudinal Wave In the longitudinal wave above, the particle on the far left vibrates horizontally in simple harmonic motion
, causing the particles to its right to also vibrate in simple harmonic motion
. The energy of the wave is transferred horizontally to the right

note

.
Transverse mechanical waves can only move through solids, while longitudinal waves can move through solids, liquids, and gases.

Surface waves

Surface waves: Longitudinal waves are generated in the depths of the oceans.
While water particles on the surface follow a circular path.
Sometimes parallel to the wave motion and sometimes perpendicular to the wave motion

Wave properties and terminology

Waves have properties closely related to those of particle vibrations. The period, frequency, and amplitude of a wave are defined in the same way as the frequency and amplitude of particle vibrations.:

periodic time - The time required for one complete oscillation. (SI unit of measurement second)

Frequency - the number of vibrations per second. (SI unit: Hertz or the reciprocal of a second)

wave Capacity - The maximum displacement from the equilibrium position. (SI unit: meter)

Wavelength - The distance between two successive crests or troughs (or between any two successive points of the same phase. (SI unit: meter)

To explore some of the properties of transverse and longitudinal waves. Adjust the amplitude and frequency sliders and see how the waves are affected. Press the "Play" button to animate the wave motion. Note that the entire transverse wave has a single equilibrium line, whereas in a longitudinal wave, each particle of the medium has its own equilibrium position.
The speed of a wave depends on the medium through which it travels, not on its frequency or wavelength.

The frequency of a wave is determined by the source that produces the wave - it does not depend on the medium through which the wave travels.

The wavelength of a wave depends on both the speed and frequency of the wave:

\[λ=\frac{v}{f}\]

Wave graphic representation

Wave behavior

the Waves at the border
When a wave reaches a limit, a point where the medium changes,
that is, when it moves into another medium, three things happen.
Some of the wave moves into the new medium, some of the wave is reflected back into the original medium,
and some of the wave's energy is absorbed. When the new medium is denser, the wave bounces back (a fixed barrier)
and when it is less dense, it bounces back in the same direction (a moving barrier).




The animation above shows the entire wave pulse being reflected back into the original medium. In fact,
some of the energy of the wave pulse will be transferred to the new medium,
and the reflected pulse will have a smaller amplitude (less energy) than the original pulse.
Also note that the speed of the reflected wave pulse is the same as the speed of the incident wave pulse.
The speed depends on the medium,
and the reflected pulse is still in the original medium, so it has the same speed as the incident pulse.

Use the simulation below to explore and think in more detail. It allows you to see how the incoming pulse and the reflected pulse combine to form the actual pulse seen on the string.


Constructive and destructive interference

When two or more waves interfere in the same medium at the same time, it is called wave interference. The interference process is easiest to understand by observing the overlapping wave pulses. Use the simulation below to explore wave pulse interference. Experiment with waves of different widths and heights, including negative height pulses interfering with positive height pulses.



Note that the wave pulses do not bounce off each other, instead,
they pass directly through each other and continue on their way as if nothing had happened.
This is known as the principle of independence.
The effect only appears when they interfere.
When two pulses overlap, the resulting wave is the algebraic sum of the two pulses.
This is known as the principle of superposition.
The principle of superposition can be stated as follows: The displacement of the medium from the equilibrium position when multiple waves overlap is equal to the algebraic sum of the displacements of the individual waves.
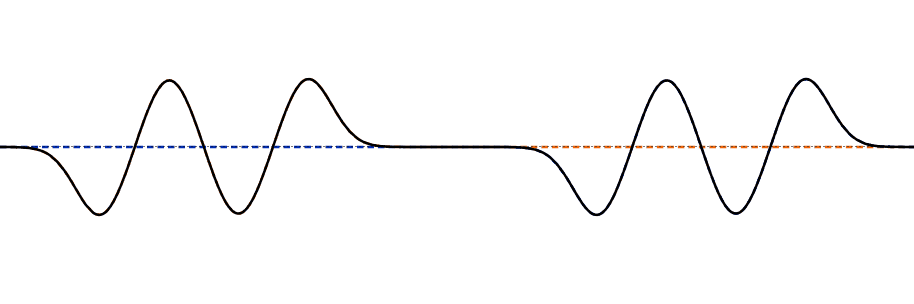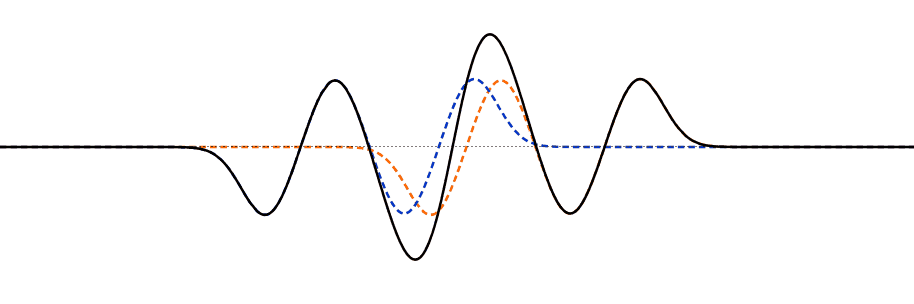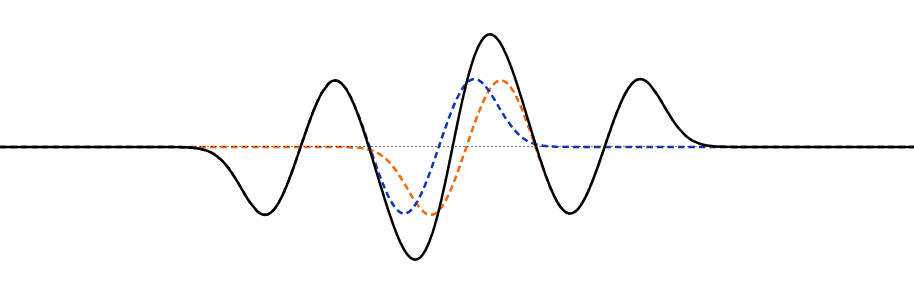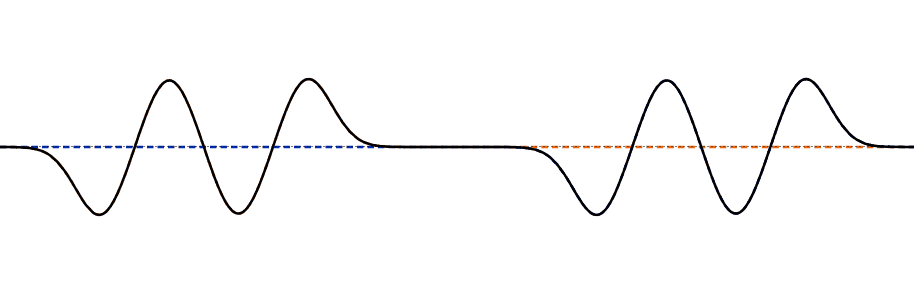
Multiple pulse interference

When multiple pulses overlap, the principle of superposition applies.
The principle of independence The colored dotted lines in the animation show the original shape of the pulses,
while the black line shows the actual appearance we see, which is the sum of the original pulses.



Many different superposition patterns can appear when two waves interfere. Here are some examples.



In the simulation above, the blue and red waves are moving in the same direction in the same medium (and therefore have the same speed).
The purple wave at the bottom shows the sum of the blue and red waves.
Use the checkbox to see the red and blue waves superimposed on each other.
Use the play button in the lower left corner to play the animation.
By default, the red and blue waves have the same wavelength and are "in phase".
When the transverse waves are in phase, they match crest to crest. The sum of the two waves has twice the amplitude of either of the original waves.
This is called constructive interference. Use the slider to change the phase of the blue wave.
Watch how their sum gets smaller as the phase difference increases. It is possible, however, that destructive interference occurs, and the two waves cancel out completely.

Now set the two wavelengths to very different values, for example try 1.5 for one and 2.5 for the other. Their sum is now shown next to each of the individual waves. It can lead to the creation of very complex wave combinations.

When two waves move in the same medium but in opposite directions, different interference patterns are formed. If the two waves moving in opposite directions have the same wavelength, the interference pattern known as a standing wave


In the simulation above, the red and blue waves are moving in the same medium,
but in opposite directions. When two waves have different wavelengths, their sum is a complex traveling wave.
Now set both wavelengths to the same value (this can also be done by clicking the Show Standing Wave button).
Their sum is a special type of wave interference known as a standing wave.
A standing wave is called a standing wave because it is not moving in either direction.
Some points on a standing wave are not moving at all, and these points are called nodes.
The points on a standing wave that undergo the greatest displacement are called antinodes.
Use the checkbox to observe the nodes and antinodes.

standing waves

When a standing wave is formed on a string, there is always a node at each end. .
This is also known as the first harmonic
First harmonic: The length of the string is equal to half the wavelength of the standing wave,
because the distance from one node to the next nearest node is half a wavelength.
The frequency of the first standing wave is called the fundamental frequency
For the first harmonic, The length of the string is equal to half the wavelength of the standing wave,
because the distance from one node to the next nearest node is half a wavelength.
The frequency of the first standing wave is called the fundamental frequency

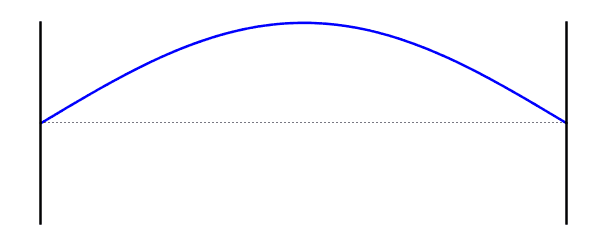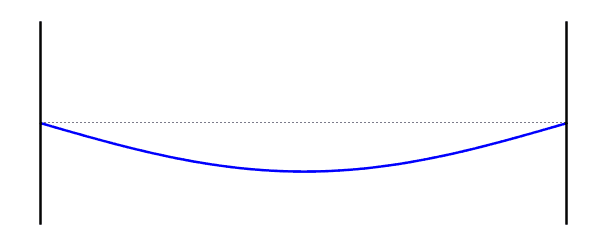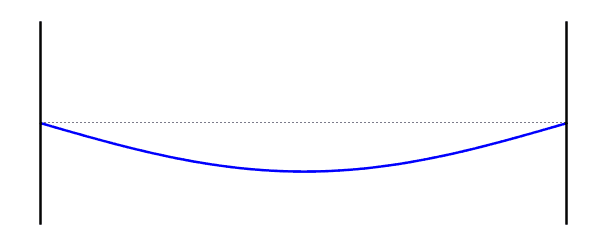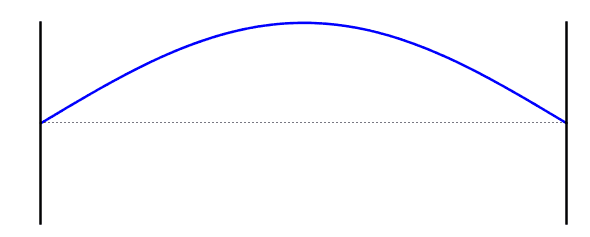
التردد الأساسي (الموجة الواقفة الاولى) \[f = f_0 \]\[L =\frac{ λ}{2}\]\[ λ = 2L\]
There are several other modes of vibration of a string fixed at each end.
Each mode is called a harmonic. At the second harmonic, the standing wave consists of two parts.
The wavelength is half the wavelength of the fundamental,
so the frequency is twice the frequency of the fundamental wave.
الموجة التوافقية الثانية
\[f = 2f_0\] \[L = λ\] \[ λ = L \]
At the third harmonic, the standing wave consists of three parts.
The wavelength is one-third the fundamental wavelength,
so the frequency is three times the fundamental wave frequency.

الموجة التوافقية الثالثة
\[f = 3f_0\] \[L = \frac{3λ}{2}\] \[λ = \frac{2L}{3}\]

Waves traveling in two dimensions

Think of a pebble dropped into a pond. The water is pushed down and then bounces back up.
This causes concentric circles to radiate outward, as shown in this diagram.
The rings form as the water level rises and falls..
The white lines are called the wave front and the black lines represent the wave trough. Each loop is a set of points that the vibration reaches in the same time period.
We call the distance between one wave front and the next wave front the wavelength.
Or the distance between two successive troughs the wavelength.
The wave propagates in all directions and the direction of wave propagation is always perpendicular to the wave front.

Reflection of waves in two dimensions

When mechanical waves strike an obstacle, at least some of the wave energy will be reflected back into the medium it came from
When a wave hits an obstacle or reaches the end of the medium it is traveling through,
some of the wave is reflected back into the original medium. It is reflected back at an angle equal to the angle of incidence. These angles are called the angle of incidence and the angle of reflection.
The normal, incident rays, reflection, angles of incidence, and reflection are shown in this simulation. The law of reflection states that the angle of incidence equals the angle of reflection.
The rules of reflection apply and this is what happens when water waves bounce off the side of a pond

Wave refraction in two dimensions

How does a wave behave when it moves from one medium to another and not perpendicular to the interface between the two media. Refraction of waves: It is the bending of waves as they pass from one medium to another. When a wave hits the surface of a different medium, some of it is reflected, while some of it bends and changes its direction as it travels through the medium. A light ray passes from air to water. Note that water has a higher refractive index than air.
Therefore, the light ray is slower in water than in air. The broken line perpendicular to the air-water interface is called the perpendicular to the surface.
The light that passes through the air and falls on the air-water boundary is called the incident ray.
While the ray after passing through the second medium is called the refracted ray.
The angle that the incident ray makes with the perpendicular to the surface is called the angle of incidence. When light passes from a material with a smaller refractive index to a material with a higher value,
its speed decreases and the refracted ray changes its normal direction. The angle between the refracted ray and the normal to the surface is called the angle of refraction, .
If a ray of light passes from water to air instead, its direction also changes. Its speed increases as it moves from a material with a higher refractive index to a material with a lower one. In this case





المصدر https://ophysics.com/em4.html اكتب تعليق أو إذا كان هناك خطأ Write a comment or if there is an error

No comments:

Post a Comment