00971504825082
Generators and Self & Mutual Induction |
Electromagnetic Induction Phenomenon

When a conducting wire moves cutting through magnetic field lines
and is part of a closed circuit
an induced electromotive force is generated between the wire ends
and an induced current flows
The reason is due to
when the conducting wire moves cutting through
magnetic field lines, electrons are affected by a magnetic force
and pushed towards one end of the wire
leaving positive charges at the other end
creating an increasing electric field
that exerts an increasing electric force on the charges in the wire opposing the magnetic force
until the two forces balance
\[ Fe = FB\] \[ q . E = q . 𝜗 . B\]\[E = 𝜗 . B \]\[B.𝜗 = \frac{{{∆𝑉}}}{{{𝐿}}} \]\[∆𝑉_{𝑖𝑛𝑑} = {{{ B . L . 𝜗 }}} \]\[∆𝑉_{𝑖𝑛𝑑} = {{{ B . L . 𝜗.Sin (θ ) }}}\](θ: angle between wire velocity and field)
If the wire is part of a closed circuit
current flows from outside the wire from positive to negative pole
and inside the wire from negative to positive pole

Example 1
A conducting wire of length
\[0.2 \;m\] was moved to cut through magnetic field lines with a velocity perpendicular to the field of
\[20\; m/S\] on a frictionless track connected to a resistor
of \[5\; Ω \]. If the magnetic field strength is
\[B=0.2\;T\], then the induced current through the resistor equals

\[I_{ind}=1\;\; A\;\;\;\;\;\;-C\]
\[I_{ind}=0.48\;\; A\;\;\;\;\;\;-A\]
\[I_{ind}=0.3\;\; A\;\;\;\;\;\;-D\]
\[I_{ind}=0.16\;\; A\;\;\;\;\;-B\]
 Click here to show solution
Click here to show solution
Choose the correct answer

Example 2
A helicopter with aluminum blades of length
8 m
flies horizontally over the UAE in a magnetic field region of strength
0.4 × 10–4 T
and rotates with angular speed of
200 rad / s
The induced potential difference generated from the axis to the end of the blade equals

\[\Delta V_{ind}=0.032\;\; V\;\;\;\;\;\;-C\]
\[\Delta V_{ind}=0.254\;\; V\;\;\;\;\;\;-A\]
\[\Delta V_{ind}=0.128\;\; V\;\;\;\;\;\;-D\]
\[\Delta V_{ind}=0.064\;\; V\;\;\;\;\;-B\]
 Click here to show solution
Click here to show solution
Choose the correct answer

Generators and Motors
Who am I 
A device that converts electrical energy to mechanical energy 
..............................
A device that converts mechanical energy to electrical energy 
..............................
To make the coil rotate in the magnetic field, different energy sources are used practically
Solar energy 
Wind energy 
Hydropower 
Fossil fuels 
Gas and oil energy 
Wastewater energy 
Nuclear energy 
A generator is a device that converts mechanical energy into electrical energy. It does this by changing the magnetic flux through a coil, inducing an electromotive force between the coil ends. Theoretically, the flux can be changed either by moving a magnet relative to the coil or moving the coil relative to the magnet. The second method is practically easier and more commonly used.
There are two types of generators:
(AC) Alternating current generator
(DC) Direct current generator
Example 3
A coil with 20 turns rotates in a magnetic field at a constant rate with its axis perpendicular to the field. The relationship between flux and time was plotted resulting in the following graph. The maximum induced potential difference in the coil equals

\[\Delta V_{max}=6.7\;\; V\;\;\;\;\;\;-C\]
\[\Delta V_{max}=5.3\;\; V\;\;\;\;\;\;-A\]
\[\Delta V_{max}=0.79\;\; V\;\;\;\;\;\;-D\]
\[\Delta V_{max}=4.2\;\; V\;\;\;\;\;-B\]
 Click here to show solution
Click here to show solution
Choose the correct answer

Useful information: Induced electric field
When flux changes on a coil, an induced potential difference is generated which in turn generates an induced current and creates an induced electric field
Consider a charge moving in a circular path in a constant electric field parallel to one of the field lines. The work done on the charge is:
\[W =\oint \vec F \cdot d\vec S=\oint q.\vec E \cdot d\vec S = q.\vec E \oint \cdot d\vec S= q.\vec E .2𝜋 .r \]
\[W =q .∆𝑉_𝑖𝑛𝑑 \]
\[ ∆𝑉_𝑖𝑛𝑑 = \vec E .2𝜋 .r =\oint \vec E \cdot d\vec S\]
\[ \oint \vec E \cdot d\vec S = -d\frac{{{ф_B}}}{{{dt}}} \]

Self Induction Phenomenon
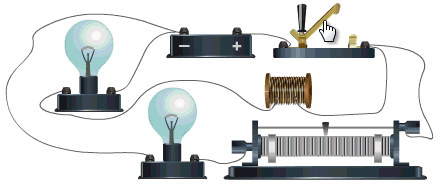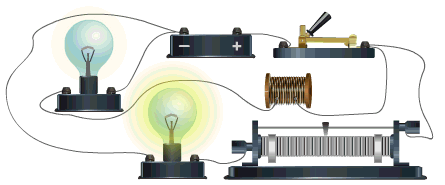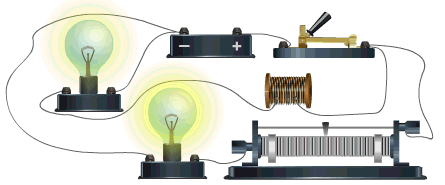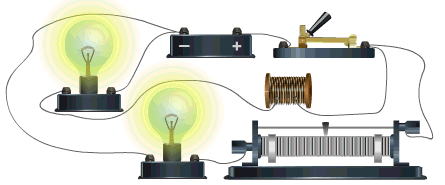
In the adjacent circuit, when the switch is closed, an induced electromotive force is generated in the coil opposing the cause due to the changing current in the coil, causing the current to grow gradually in the circuit.

When the circuit is opened, the current decreases gradually in the coil due to the generation of an opposing electromotive force similar to the cause, delaying the current decay.
\[ ∆𝑉_𝑖𝑛𝑑 =- L .d\frac{{{i}}}{{{dt}}} \] Self-inductance coefficient of the coil measured in Henry (L)
\[ ∆𝑉_𝑖𝑛𝑑 =- N .d\frac{{{ф_B}}}{{{dt}}} \]
\[- L .d\frac{{{i}}}{{{dt}}}=- N .d\frac{{{ф_B}}}{{{dt}}} \]
\[ L .{{{i}}}= N .{{{ф}}} \]
\[ф=A.B=A.\frac{\mu_0Ni}{𝑙} \]
\[ L .{{{i}}}= N .{{{A.\frac{\mu_0Ni}{𝑙}}}} \]
\[ L = {{{\frac{\mu_0N^2.A}{𝑙}}}}={{{{\mu_0.n^2.A.𝑙}}}} \] where n is the number of turns per unit length
Self-induction delays the growth and decay of current
In the animation, there are two bulbs - the upper one is connected to a coil and the lower one to a resistor. The coil delays the bulb lighting when the circuit is closed.
Example 4

A coil with 20 turns has self-inductance coefficient
\[0.4\; H\]. If 8 turns are removed, its self-inductance coefficient becomes

\[L=0.24\;\;H\;\;\;\;\;\;-C\]
\[L=0.32\;\;H\;\;\;\;\;\;-A\]
\[L=0.16\;\;H\;\;\;\;\;\;-D\]
\[L=0.22\;\;H\;\;\;\;\;-B\]
 Click here to show solution
Click here to show solution
Choose the correct answer

Mutual Induction Phenomenon
In this simulation, when circuit 1 is closed, the current won't reach its maximum value immediately but gradually due to self-induction. The field changes on coil 2 inducing a mutual potential difference. Also due to self-induction in coil 2, the current won't reach its maximum immediately, changing the field on coil 1 and inducing a potential difference. This is known as self and mutual induction.
Observe mutual induction when closing/opening circuit 1
and when increasing/decreasing the variable resistor in circuit 1
and when increasing/decreasing the battery voltage in circuit 1
Mutual inductance coefficient (M) is the effect of the second circuit on the first in the primary coil where:
\[ ∆𝑉_{𝑖𝑛𝑑1} =-𝑀 .d\frac{{{𝑖_2}}}{{{dt}}}=- N_1 .d\frac{{{ф_1}}}{{{dt}}} \]
Mutual inductance coefficient (M) is the effect of the first circuit on the second in the secondary coil where:
\[ ∆𝑉_{𝑖𝑛𝑑2} =- 𝑀.d\frac{{{𝑖_1}}}{{{dt}}}=- N_2 .d\frac{{{ф_2}}}{{{dt}}} \]
Mutual inductance coefficient effect of first on second = mutual inductance coefficient effect of second on first

Source
https://seilias.gr/go-lab/html5/faraday2.plain.html
🧮 Calculator
🗑️
✏️ قلم
Electromagnetic Induction Phenomenon

and is part of a closed circuit
an induced electromotive force is generated between the wire ends
and an induced current flows
The reason is due to
when the conducting wire moves cutting through
magnetic field lines, electrons are affected by a magnetic force
and pushed towards one end of the wire
leaving positive charges at the other end
creating an increasing electric field
that exerts an increasing electric force on the charges in the wire opposing the magnetic force
until the two forces balance \[ Fe = FB\] \[ q . E = q . 𝜗 . B\]\[E = 𝜗 . B \]\[B.𝜗 = \frac{{{∆𝑉}}}{{{𝐿}}} \]\[∆𝑉_{𝑖𝑛𝑑} = {{{ B . L . 𝜗 }}} \]\[∆𝑉_{𝑖𝑛𝑑} = {{{ B . L . 𝜗.Sin (θ ) }}}\](θ: angle between wire velocity and field)
If the wire is part of a closed circuit
current flows from outside the wire from positive to negative pole
and inside the wire from negative to positive pole
A conducting wire of length \[0.2 \;m\] was moved to cut through magnetic field lines with a velocity perpendicular to the field of \[20\; m/S\] on a frictionless track connected to a resistor of \[5\; Ω \]. If the magnetic field strength is \[B=0.2\;T\], then the induced current through the resistor equals

\[I_{ind}=1\;\; A\;\;\;\;\;\;-C\] |
\[I_{ind}=0.48\;\; A\;\;\;\;\;\;-A\] |
\[I_{ind}=0.3\;\; A\;\;\;\;\;\;-D\] |
\[I_{ind}=0.16\;\; A\;\;\;\;\;-B\] |
 Click here to show solution
Click here to show solution
Choose the correct answer
A helicopter with aluminum blades of length
8 m
flies horizontally over the UAE in a magnetic field region of strength
0.4 × 10–4 T
and rotates with angular speed of
200 rad / s
The induced potential difference generated from the axis to the end of the blade equals

\[\Delta V_{ind}=0.032\;\; V\;\;\;\;\;\;-C\] |
\[\Delta V_{ind}=0.254\;\; V\;\;\;\;\;\;-A\] |
\[\Delta V_{ind}=0.128\;\; V\;\;\;\;\;\;-D\] |
\[\Delta V_{ind}=0.064\;\; V\;\;\;\;\;-B\] |
 Click here to show solution
Click here to show solution
Choose the correct answer
Generators and Motors
Who am I A device that converts electrical energy to mechanical energy ..............................
A device that converts mechanical energy to electrical energy ..............................
To make the coil rotate in the magnetic field, different energy sources are used practically
Solar energy Wind energy Hydropower Fossil fuels Gas and oil energy Wastewater energy Nuclear energy A coil with 20 turns rotates in a magnetic field at a constant rate with its axis perpendicular to the field. The relationship between flux and time was plotted resulting in the following graph. The maximum induced potential difference in the coil equals \[\Delta V_{max}=6.7\;\; V\;\;\;\;\;\;-C\]
\[\Delta V_{max}=5.3\;\; V\;\;\;\;\;\;-A\]
\[\Delta V_{max}=0.79\;\; V\;\;\;\;\;\;-D\]
\[\Delta V_{max}=4.2\;\; V\;\;\;\;\;-B\]
Choose the correct answer
When flux changes on a coil, an induced potential difference is generated which in turn generates an induced current and creates an induced electric field
Consider a charge moving in a circular path in a constant electric field parallel to one of the field lines. The work done on the charge is:
\[W =\oint \vec F \cdot d\vec S=\oint q.\vec E \cdot d\vec S = q.\vec E \oint \cdot d\vec S= q.\vec E .2𝜋 .r \]
\[W =q .∆𝑉_𝑖𝑛𝑑 \]
\[ ∆𝑉_𝑖𝑛𝑑 = \vec E .2𝜋 .r =\oint \vec E \cdot d\vec S\]
\[ \oint \vec E \cdot d\vec S = -d\frac{{{ф_B}}}{{{dt}}} \]
In the adjacent circuit, when the switch is closed, an induced electromotive force is generated in the coil opposing the cause due to the changing current in the coil, causing the current to grow gradually in the circuit.
When the circuit is opened, the current decreases gradually in the coil due to the generation of an opposing electromotive force similar to the cause, delaying the current decay.
\[ ∆𝑉_𝑖𝑛𝑑 =- L .d\frac{{{i}}}{{{dt}}} \] Self-inductance coefficient of the coil measured in Henry (L)
\[ ∆𝑉_𝑖𝑛𝑑 =- N .d\frac{{{ф_B}}}{{{dt}}} \]
\[- L .d\frac{{{i}}}{{{dt}}}=- N .d\frac{{{ф_B}}}{{{dt}}} \]
\[ L .{{{i}}}= N .{{{ф}}} \]
\[ф=A.B=A.\frac{\mu_0Ni}{𝑙} \]
\[ L .{{{i}}}= N .{{{A.\frac{\mu_0Ni}{𝑙}}}} \]
\[ L = {{{\frac{\mu_0N^2.A}{𝑙}}}}={{{{\mu_0.n^2.A.𝑙}}}} \] where n is the number of turns per unit length
Self-induction delays the growth and decay of current
In the animation, there are two bulbs - the upper one is connected to a coil and the lower one to a resistor. The coil delays the bulb lighting when the circuit is closed.
A coil with 20 turns has self-inductance coefficient
\[0.4\; H\]. If 8 turns are removed, its self-inductance coefficient becomes
\[L=0.24\;\;H\;\;\;\;\;\;-C\]
\[L=0.32\;\;H\;\;\;\;\;\;-A\]
\[L=0.16\;\;H\;\;\;\;\;\;-D\]
\[L=0.22\;\;H\;\;\;\;\;-B\]
Choose the correct answer In this simulation, when circuit 1 is closed, the current won't reach its maximum value immediately but gradually due to self-induction. The field changes on coil 2 inducing a mutual potential difference. Also due to self-induction in coil 2, the current won't reach its maximum immediately, changing the field on coil 1 and inducing a potential difference. This is known as self and mutual induction.
Mutual inductance coefficient (M) is the effect of the second circuit on the first in the primary coil where:
\[ ∆𝑉_{𝑖𝑛𝑑1} =-𝑀 .d\frac{{{𝑖_2}}}{{{dt}}}=- N_1 .d\frac{{{ф_1}}}{{{dt}}} \]
Mutual inductance coefficient (M) is the effect of the first circuit on the second in the secondary coil where:
\[ ∆𝑉_{𝑖𝑛𝑑2} =- 𝑀.d\frac{{{𝑖_1}}}{{{dt}}}=- N_2 .d\frac{{{ф_2}}}{{{dt}}} \]
Mutual inductance coefficient effect of first on second = mutual inductance coefficient effect of second on first










A generator is a device that converts mechanical energy into electrical energy. It does this by changing the magnetic flux through a coil, inducing an electromotive force between the coil ends. Theoretically, the flux can be changed either by moving a magnet relative to the coil or moving the coil relative to the magnet. The second method is practically easier and more commonly used.
There are two types of generators:
(AC) Alternating current generator
(DC) Direct current generator


Useful information: Induced electric field
Self Induction Phenomenon




Mutual Induction Phenomenon
Observe mutual induction when closing/opening circuit 1
and when increasing/decreasing the variable resistor in circuit 1
and when increasing/decreasing the battery voltage in circuit 1
 Physics
Physics

No comments:
Post a Comment