📄 Print pdf
00971504825082
(11 A ) Question Bank: Motion in One Dimension
\[1 \star \]
Ahmed moved east a distance of
\[80 \;\;m\]
then continued in the same direction a distance of \[50\;\;m\] then changed direction and traveled a distance
\[160\;\;m\] west. The distance and displacement traveled are:
Click here to show solution
Choose the correct answer
\[ 𝑆=290 m\;\;\; , \;\;\;∆𝑥=30 m\;\;\;\;\;\;-C\]
east
\[ 𝑆=30 m\;\;\; , \;\;\;∆𝑥=290 m \;\;\;\;\;\;-A\]
west
\[ 𝑆=30 m\;\;\; , \;\;\;∆𝑥=290 m\;\;\;\;\;\;-D\]
east
\[ 𝑆=290 m\;\;\; , \;\;\;∆𝑥=30 m\;\;\;\;\;\;-B\]
west
\[2 \star \]
The position-time graph for a bicycle is shown in the adjacent figure. The distance traveled and displacement during the entire period are equal to:
\[ 𝑆=20 m\;\;\; , \;\;\;∆𝑥=4 m\;\;\;\;\;\;-C\]
\[ 𝑆=20 m\;\;\; , \;\;\;∆𝑥=-8 m \;\;\;\;\;\;-A\]
\[ 𝑆=28 m\;\;\; , \;\;\;∆𝑥=4 m\;\;\;\;\;\;-D\]
\[ 𝑆=28 m\;\;\; , \;\;\;∆𝑥=-4 m\;\;\;\;\;\;-B\]
Click here to show solution
Choose the correct answer
\[3 \star \]
The position-time graph for a bicycle resulted in the following graph. The distance traveled and displacement are equal to:
\[ 𝑆=25 m\;\;\; , \;\;\;∆𝑥=-10 m\;\;\;\;\;\;-C\]
\[ 𝑆=20 m\;\;\; , \;\;\;∆𝑥=-15 m \;\;\;\;\;\;-A\]
\[ 𝑆=10 m\;\;\; , \;\;\;∆𝑥=10 m\;\;\;\;\;\;-D\]
\[ 𝑆=25 m\;\;\; , \;\;\;∆𝑥=-15 m\;\;\;\;\;\;-B\]
Click here to show solution
Choose the correct answer
\[4 \star \]
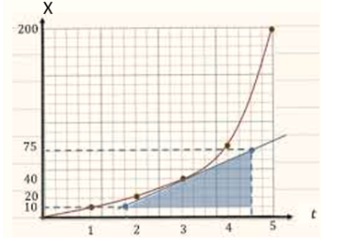
The position equation for a car moving in one dimension:
\[𝑋(𝑡)=𝑡^3−5𝑡^2+15𝑡\]
The instantaneous velocity at the fourth second
\[t=4 s\]
\[ 𝑣(𝑡)=23\;\; m/s \;\;\;\;\;\;-C\]
\[ 𝑣(𝑡)=20\;\; m/s \;\;\;\;\;\;-A\]
\[ 𝑣(𝑡)=15\;\; m/s \;\;\;\;\;\;-D\]
\[ 𝑣(𝑡)=18\;\; m/s \;\;\;\;\;\;-B\]
Click here to show solution Choose the correct answer
\[5 \star \]
The position equation for a rocket launched vertically in one axis
\[Y(𝑡)=3t^3−6𝑡^2+5 \]
then the average velocity between the moments \[t=5 s , t=8 s\]
\[ 𝑣_{𝑎𝑣𝑟𝑔}= 309 \;\;𝑚/𝑠\;\;\;\;\;\;-C\]
\[ 𝑣_{𝑎𝑣𝑟𝑔}= 115 \;\;𝑚/𝑠\;\;\;\;\;\;-A\]
\[ 𝑣_{𝑎𝑣𝑟𝑔}= 236 \;\;𝑚/𝑠\;\;\;\;\;\;-D\]
\[ 𝑣_{𝑎𝑣𝑟𝑔}= 205 \;\;𝑚/𝑠\;\;\;\;\;\;-B\]
Click here to show the solution
Choose the correct answer
\[6 \star \]
The slope of the tangent to the position-time graph represents
Instantaneous acceleration-C
Average acceleration-A
Instantaneous velocity -D
Average velocity
-B
Click here to show the solution
Choose the correct answer
\[7 \star \]
The position-time graph for a bicycle is shown
The average velocity during the entire period equals
\[ 𝑣_{𝑎𝑣𝑟𝑔}= 0.12 \;\;𝑚/𝑠\;\;\;\;\;\;-C\]
\[ 𝑣_{𝑎𝑣𝑟𝑔}=0.67 \;\;𝑚/𝑠\;\;\;\;\;\;-A\]
\[ 𝑣_{𝑎𝑣𝑟𝑔}= 0.39 \;\;𝑚/𝑠\;\;\;\;\;\;-D\]
\[ 𝑣_{𝑎𝑣𝑟𝑔}= 0.85 \;\;𝑚/𝑠\;\;\;\;\;\;-B\]
Click here to show the solution
Choose the correct answer
\[8 \star\]
A car starts from rest with a constant acceleration of
\[2\;\;m/s^2\] then its speed after covering a distance of
\[20\;\;m\]
equals
\[ 𝑣_{f}= 12.2 \;\;𝑚/𝑠\;\;\;\;\;\;-C\]
\[ 𝑣_{f}=4.6 \;\;𝑚/𝑠\;\;\;\;\;\;-A\]
\[ 𝑣_{f}= 6.7 \;\;𝑚/𝑠\;\;\;\;\;\;-D\]
\[ 𝑣_{f}= 8.9 \;\;𝑚/𝑠\;\;\;\;\;\;-B\]
Click here to show the solution
Choose the correct answer
\[9 \star \]
One of the following equations expresses the position as a function of time for an object moving with constant acceleration
Click here to show the solution
Choose the correct answer
\[10 \star \]
A car slows down until it comes to a complete stop. The figure shows a series of sequential images
of this process. The time between two consecutive images is
\[0.4 \;\;s\]
and the length of the car is
\[2.5\;\;m\]
Based on the figure data and the written information, the car
is moving with a constant acceleration of
\[a=−1.7\;\; 𝑚/𝑠^2\;\;\;\;\;\;-C\]
\[a=−3.5\;\; 𝑚/𝑠^2\;\;\;\;\;\;-A\]
\[a=−0.9\;\; 𝑚/𝑠^2\;\;\;\;\;\;-D\]
\[a=−2.6\;\; 𝑚/𝑠^2\;\;\;\;\;\;-B\]
Click here to show the solution
Choose the correct answer
>\[11 \star \]
The graph describes the position of an object moving in one dimension
as a function of time. During which time interval does the object reach maximum velocity?
\[t=5 \;S \longrightarrow t=7 \;S\;\;\;\;\;\;-C\]
\[t=0 \;S \longrightarrow t=3 \;S \;\;\;\;\;\;-A\]
\[t=7 \;S \longrightarrow t=10 \;S\;\;\;\;\;\;-D\]
\[t=3 \;S \longrightarrow t=5 \;S\;\;\;\;\;\;-B\]
Click here to show solution Choose the correct answer
>\[12 \star \]
A stone is thrown vertically upward with an initial velocity. The acceleration of the stone at the moment it reaches maximum height equals:
\[a=−9.81\;\; 𝑚/𝑠^2\;\;\;\;\;\;-C\]
\[a=0\;\; 𝑚/𝑠^2\;\;\;\;\;\;-A\]
\[a=4\;\; 𝑚/𝑠^2\;\;\;\;\;\;-D\]
\[a=2\;\; 𝑚/𝑠^2\;\;\;\;\;\;-B\]
Click here to show solution Choose the correct answer
>\[13 \star \]
The graph shows the relationship between velocity and time for a car
From the graph, the distance traveled equals:
\[∆𝑥=250\;\; m\;\;\;\;\;\;-C\]
\[ ∆𝑥=50\;\; m\;\;\;\;\;\;-A\]
\[∆𝑥=100\;\; m\;\;\;\;\;\;-D\]
\[∆𝑥=200\;\; m\;\;\;\;\;\;-B\]
Click here to show solution Choose the correct answer
>\[14 \star \]
A car is moving with velocity
\[2\;\;m/s\] when the driver changes its speed at a rate of
\[0.5\;\;m/s^2\]. The distance traveled in
\[1\;\;min\]
equals
\[∆𝑥=1250\;\; m\;\;\;\;\;\;-C\]
\[ ∆𝑥=850\;\; m\;\;\;\;\;\;-A\]
\[∆𝑥=1020\;\; m\;\;\;\;\;\;-D\]
\[∆𝑥=730\;\; m\;\;\;\;\;\;-B\]
Click here to show solution Choose the correct answer
>\[15 \star \]
The graph shows the relationship between (velocity - time)
for an object thrown upward with an initial
velocity in one dimension
The best graph showing the relationship between
(acceleration - time) for this motion
Click here to show solution
Choose the correct answer
>\[16 \star \]
The graph shows the relationship between velocity
and time for a bicycle
One part of the graph shows an object moving with zero acceleration
\[3\;\;\;\;\;\;-C\]
\[1\;\;\;\;\;\;-A\]
\[4\;\;\;\;\;\;-D\]
\[2\;\;\;\;\;\;-B\]
Click here to show the solution
Choose the correct answer
>\[17 \star \]
The following graph shows the relationship between (velocity - time)
for a bicycle moving in one dimension
Calculate the average acceleration between the time period
\[t=4 s\longrightarrow t=8 s\]
\[a=3\;\; 𝑚/𝑠^2\;\;\;\;\;\;-C\]
\[a=1\;\; 𝑚/𝑠^2\;\;\;\;\;\;-A\]
\[a=4\;\; 𝑚/𝑠^2\;\;\;\;\;\;-D\]
\[a=2\;\; 𝑚/𝑠^2\;\;\;\;\;\;-B\]
Click here to show the solution
Choose the correct answer
>\[18 \star \]
The following graph shows the relationship between (velocity - time)
for a bicycle moving in one dimension
Calculate the instantaneous acceleration at the moment
\[ t=8 s\]
\[a_i=4.5\;\; 𝑚/𝑠^2\;\;\;\;\;\;-C\]
\[a_i=2.5\;\; 𝑚/𝑠^2\;\;\;\;\;\;-A\]
\[a_i=5.5\;\; 𝑚/𝑠^2\;\;\;\;\;\;-D\]
\[a_i=3.5\;\; 𝑚/𝑠^2\;\;\;\;\;\;-B\]
Click here to show the solution
Choose the correct answer
>\[19 \star \]
A ball was thrown vertically upwards and at three-quarters of its maximum height its speed was
\[12\;\;m/s\]
The maximum height the ball reaches is
\[ℎ=29.4 \;\;𝑚\;\;\;\;\;\;-C\]
\[ ℎ=19.3 \;\;𝑚 \;\;\;\;\;\;-A\]
\[ℎ=12.8 \;\;𝑚\;\;\;\;\;\;-D\]
\[ℎ=22.5 \;\;𝑚\;\;\;\;\;\;-B\]
Click here to show the solution
Choose the correct answer
>\[20 \star \]
In a football game during the match, an attacking player moved towards the opponent's goal to the east for a distance of
\[50\;\; m\]
in a straight line
during a time of
\[t=8 \;\;s\] then the ball bounced back and moved in the opposite direction covering a distance of
\[30\;\; m\] during a time of
\[10\;\;s\]
The average speed during the attack phase, the average speed during the bounce phase, and the average speed for the entire period equal
\[𝑣_1=3.33 m/s\;\;,\;\; 𝑣_2=1.7 m/s\;\;,\;\;𝑣=-4.44 m/s\;\;\;\;\;\;-C\]
\[𝑣_1=3.33 m/s\;\;,\;\; 𝑣_2=-3 m/s\;\;,\;\;𝑣=4.44 m/s\;\;\;\;\;\;-A\]
\[𝑣_1=6.25 m/s\;\;,\;\; 𝑣_2=-3 m/s\;\;,\;\;𝑣=1.11 m/s\;\;\;\;\;\;-D\]
\[𝑣_1=6.25 m/s\;\;,\;\; 𝑣_2=3 m/s\;\;,\;\;𝑣=4.44 m/s\;\;\;\;\;\;-B\]
Click here to show solution
Choose the correct answer
>\[21 \star \]
The graph shows the relationship between velocity and time for a bicycle moving in one dimension
The best graph that shows the relationship between
acceleration and time for this motion
Click here to show solution
Choose the correct answer
>\[22 \star \]
The graph shows the relationship between
(Position - Time)
for the motion of a tractor
At what moment was the velocity zero and at what moment was the acceleration zero
\[(𝑣=0 →𝑡=10 𝑠)(𝑎=0 →𝑡=35 𝑠)\;\;\;\;\;\;-C\]
\[ (𝑣=0 →𝑡=20 𝑠)(𝑎=0 →𝑡=20 𝑠)\;\;\;\;\;\;-A\]
\[ (𝑣=0 →𝑡=20 𝑠)(𝑎=0 →𝑡=30 𝑠) \;\;\;\;\;\;-D\]
\[ (𝑣=0 →𝑡=35 𝑠)(𝑎=0 →𝑡=20 𝑠) \;\;\;\;\;\;-B\]
Click here to show solution
Choose the correct answer
>\[23 \star \]
The following graph shows the relationship between (Velocity - Time) for a car's motion
Calculate the displacement of the car from second
\[t=15 \;\;s\Rightarrow t=40\;\;s\]
Click here to show solution
Choose the correct answer
Solve the Following Problems
1
( X ) Determines the position of a body moving on the axis
through the relationship
\[X=9−10 𝑡+2𝑡^2 \] where \[X(m) , t(s) \] Determine the position of the body when it reaches maximum displacement
\[........................................................................................\]
\[........................................................................................\]
\[........................................................................................\]
\[........................................................................................\]
\[........................................................................................\]
Click here to show the solution method
2
A red car was standing on the side of the road when a blue car passed by moving at a constant speed
\[20 \;\;m/s\] At that moment, the red car started moving with a constant acceleration of
\[3\;\;m/s^2\]
How much time does the red car need to catch up with the blue car?
\[........................................................................................\]
\[........................................................................................\]
\[........................................................................................\]
What is the distance traveled by the red car until it reaches the blue car?
\[........................................................................................\]
\[........................................................................................\]
Click here to show the solution method
3
An airplane landed on a runway and touched the ground at a speed of
\[50\;\;m/s\] moving with constant deceleration and stopped at a distance of
\[700 \;\;m\] What was its speed after moving on the runway
\[500\;\;m\]
\[........................................................................................\]
\[........................................................................................\]
\[........................................................................................\]
\[........................................................................................\]
\[........................................................................................\]
Click here to show the solution method
4
A ball was thrown from the ground surface with an initial speed of
\[20\;\;m/s\] Calculate the speed of the ball at half of the maximum height (neglecting air resistance)
\[g=9.81 m/s^2\]
\[........................................................................................\]
\[........................................................................................\]
\[........................................................................................\]
\[........................................................................................\]
\[........................................................................................\]
Click here to show the solution method
5
A balloon is stationary at a height of
\[40\;\;m\] from the ground surface
A ball was dropped to fall freely vertically to the ground
At the same moment the ball was dropped, an arrow was fired from
the ground surface vertically at the ball with a speed of
\[30\;\;m/s\]
At what height will the ball and arrow meet?
\[........................................................................................\]
\[........................................................................................\]
\[........................................................................................\]
\[........................................................................................\]
\[........................................................................................\]
Click here to show the solution method
(11 A ) Question Bank: Motion in One Dimension |
Ahmed moved east a distance of \[80 \;\;m\] then continued in the same direction a distance of \[50\;\;m\] then changed direction and traveled a distance \[160\;\;m\] west. The distance and displacement traveled are:
Click here to show solution
Choose the correct answer
\[ 𝑆=290 m\;\;\; , \;\;\;∆𝑥=30 m\;\;\;\;\;\;-C\] east |
\[ 𝑆=30 m\;\;\; , \;\;\;∆𝑥=290 m \;\;\;\;\;\;-A\] west |
\[ 𝑆=30 m\;\;\; , \;\;\;∆𝑥=290 m\;\;\;\;\;\;-D\] east |
\[ 𝑆=290 m\;\;\; , \;\;\;∆𝑥=30 m\;\;\;\;\;\;-B\] west |
The position-time graph for a bicycle is shown in the adjacent figure. The distance traveled and displacement during the entire period are equal to:
\[ 𝑆=20 m\;\;\; , \;\;\;∆𝑥=4 m\;\;\;\;\;\;-C\] |
\[ 𝑆=20 m\;\;\; , \;\;\;∆𝑥=-8 m \;\;\;\;\;\;-A\] |
\[ 𝑆=28 m\;\;\; , \;\;\;∆𝑥=4 m\;\;\;\;\;\;-D\] |
\[ 𝑆=28 m\;\;\; , \;\;\;∆𝑥=-4 m\;\;\;\;\;\;-B\] |
Click here to show solution
Choose the correct answer
The position-time graph for a bicycle resulted in the following graph. The distance traveled and displacement are equal to:
\[ 𝑆=25 m\;\;\; , \;\;\;∆𝑥=-10 m\;\;\;\;\;\;-C\] |
\[ 𝑆=20 m\;\;\; , \;\;\;∆𝑥=-15 m \;\;\;\;\;\;-A\] |
\[ 𝑆=10 m\;\;\; , \;\;\;∆𝑥=10 m\;\;\;\;\;\;-D\] |
\[ 𝑆=25 m\;\;\; , \;\;\;∆𝑥=-15 m\;\;\;\;\;\;-B\] |
Click here to show solution
Choose the correct answer
The position equation for a car moving in one dimension: \[𝑋(𝑡)=𝑡^3−5𝑡^2+15𝑡\] The instantaneous velocity at the fourth second \[t=4 s\]
\[ 𝑣(𝑡)=23\;\; m/s \;\;\;\;\;\;-C\] |
\[ 𝑣(𝑡)=20\;\; m/s \;\;\;\;\;\;-A\] |
\[ 𝑣(𝑡)=15\;\; m/s \;\;\;\;\;\;-D\] |
\[ 𝑣(𝑡)=18\;\; m/s \;\;\;\;\;\;-B\] |
Click here to show solutionChoose the correct answer
The position equation for a rocket launched vertically in one axis
\[Y(𝑡)=3t^3−6𝑡^2+5 \]
then the average velocity between the moments \[t=5 s , t=8 s\]
\[ 𝑣_{𝑎𝑣𝑟𝑔}= 309 \;\;𝑚/𝑠\;\;\;\;\;\;-C\] |
\[ 𝑣_{𝑎𝑣𝑟𝑔}= 115 \;\;𝑚/𝑠\;\;\;\;\;\;-A\] |
\[ 𝑣_{𝑎𝑣𝑟𝑔}= 236 \;\;𝑚/𝑠\;\;\;\;\;\;-D\] |
\[ 𝑣_{𝑎𝑣𝑟𝑔}= 205 \;\;𝑚/𝑠\;\;\;\;\;\;-B\] |
Click here to show the solution
Choose the correct answer
The slope of the tangent to the position-time graph represents
Instantaneous acceleration-C |
Average acceleration-A |
Instantaneous velocity -D |
Average velocity -B |
Click here to show the solution
Choose the correct answer
The position-time graph for a bicycle is shown
The average velocity during the entire period equals
\[ 𝑣_{𝑎𝑣𝑟𝑔}= 0.12 \;\;𝑚/𝑠\;\;\;\;\;\;-C\] |
\[ 𝑣_{𝑎𝑣𝑟𝑔}=0.67 \;\;𝑚/𝑠\;\;\;\;\;\;-A\] |
\[ 𝑣_{𝑎𝑣𝑟𝑔}= 0.39 \;\;𝑚/𝑠\;\;\;\;\;\;-D\] |
\[ 𝑣_{𝑎𝑣𝑟𝑔}= 0.85 \;\;𝑚/𝑠\;\;\;\;\;\;-B\] |
Click here to show the solution
Choose the correct answer
A car starts from rest with a constant acceleration of
\[2\;\;m/s^2\] then its speed after covering a distance of
\[20\;\;m\]
equals
\[ 𝑣_{f}= 12.2 \;\;𝑚/𝑠\;\;\;\;\;\;-C\] |
\[ 𝑣_{f}=4.6 \;\;𝑚/𝑠\;\;\;\;\;\;-A\] |
\[ 𝑣_{f}= 6.7 \;\;𝑚/𝑠\;\;\;\;\;\;-D\] |
\[ 𝑣_{f}= 8.9 \;\;𝑚/𝑠\;\;\;\;\;\;-B\] |
Click here to show the solution
Choose the correct answer
One of the following equations expresses the position as a function of time for an object moving with constant acceleration
Click here to show the solution
Choose the correct answer
A car slows down until it comes to a complete stop. The figure shows a series of sequential images
of this process. The time between two consecutive images is
\[0.4 \;\;s\]
and the length of the car is
\[2.5\;\;m\]
Based on the figure data and the written information, the car
is moving with a constant acceleration of
\[a=−1.7\;\; 𝑚/𝑠^2\;\;\;\;\;\;-C\] |
\[a=−3.5\;\; 𝑚/𝑠^2\;\;\;\;\;\;-A\] |
\[a=−0.9\;\; 𝑚/𝑠^2\;\;\;\;\;\;-D\] |
\[a=−2.6\;\; 𝑚/𝑠^2\;\;\;\;\;\;-B\] |
Click here to show the solution
Choose the correct answer
The graph describes the position of an object moving in one dimension
as a function of time. During which time interval does the object reach maximum velocity?
\[t=5 \;S \longrightarrow t=7 \;S\;\;\;\;\;\;-C\] |
\[t=0 \;S \longrightarrow t=3 \;S \;\;\;\;\;\;-A\] |
\[t=7 \;S \longrightarrow t=10 \;S\;\;\;\;\;\;-D\] |
\[t=3 \;S \longrightarrow t=5 \;S\;\;\;\;\;\;-B\] |
Click here to show solutionChoose the correct answer
A stone is thrown vertically upward with an initial velocity. The acceleration of the stone at the moment it reaches maximum height equals:
\[a=−9.81\;\; 𝑚/𝑠^2\;\;\;\;\;\;-C\] |
\[a=0\;\; 𝑚/𝑠^2\;\;\;\;\;\;-A\] |
\[a=4\;\; 𝑚/𝑠^2\;\;\;\;\;\;-D\] |
\[a=2\;\; 𝑚/𝑠^2\;\;\;\;\;\;-B\] |
Click here to show solutionChoose the correct answer
The graph shows the relationship between velocity and time for a car
From the graph, the distance traveled equals:
\[∆𝑥=250\;\; m\;\;\;\;\;\;-C\] |
\[ ∆𝑥=50\;\; m\;\;\;\;\;\;-A\] |
\[∆𝑥=100\;\; m\;\;\;\;\;\;-D\] |
\[∆𝑥=200\;\; m\;\;\;\;\;\;-B\] |
Click here to show solutionChoose the correct answer
A car is moving with velocity
\[2\;\;m/s\] when the driver changes its speed at a rate of
\[0.5\;\;m/s^2\]. The distance traveled in
\[1\;\;min\]
equals
\[∆𝑥=1250\;\; m\;\;\;\;\;\;-C\] |
\[ ∆𝑥=850\;\; m\;\;\;\;\;\;-A\] |
\[∆𝑥=1020\;\; m\;\;\;\;\;\;-D\] |
\[∆𝑥=730\;\; m\;\;\;\;\;\;-B\] |
Click here to show solutionChoose the correct answer
The graph shows the relationship between (velocity - time)
for an object thrown upward with an initial
velocity in one dimension
The best graph showing the relationship between
(acceleration - time) for this motion
Click here to show solution
Choose the correct answer
The graph shows the relationship between velocity
and time for a bicycle
One part of the graph shows an object moving with zero acceleration
\[3\;\;\;\;\;\;-C\] |
\[1\;\;\;\;\;\;-A\] |
\[4\;\;\;\;\;\;-D\] |
\[2\;\;\;\;\;\;-B\] |
Click here to show the solution
Choose the correct answer
The following graph shows the relationship between (velocity - time)
for a bicycle moving in one dimension
Calculate the average acceleration between the time period
\[t=4 s\longrightarrow t=8 s\]
\[a=3\;\; 𝑚/𝑠^2\;\;\;\;\;\;-C\] |
\[a=1\;\; 𝑚/𝑠^2\;\;\;\;\;\;-A\] |
\[a=4\;\; 𝑚/𝑠^2\;\;\;\;\;\;-D\] |
\[a=2\;\; 𝑚/𝑠^2\;\;\;\;\;\;-B\] |
Click here to show the solution
Choose the correct answer
for a bicycle moving in one dimension
Calculate the instantaneous acceleration at the moment \[ t=8 s\]
\[a_i=4.5\;\; 𝑚/𝑠^2\;\;\;\;\;\;-C\] |
\[a_i=2.5\;\; 𝑚/𝑠^2\;\;\;\;\;\;-A\] |
\[a_i=5.5\;\; 𝑚/𝑠^2\;\;\;\;\;\;-D\] |
\[a_i=3.5\;\; 𝑚/𝑠^2\;\;\;\;\;\;-B\] |
Click here to show the solution
Choose the correct answer
A ball was thrown vertically upwards and at three-quarters of its maximum height its speed was \[12\;\;m/s\] The maximum height the ball reaches is
\[ℎ=29.4 \;\;𝑚\;\;\;\;\;\;-C\] |
\[ ℎ=19.3 \;\;𝑚 \;\;\;\;\;\;-A\] |
\[ℎ=12.8 \;\;𝑚\;\;\;\;\;\;-D\] |
\[ℎ=22.5 \;\;𝑚\;\;\;\;\;\;-B\] |
Click here to show the solution
Choose the correct answer
In a football game during the match, an attacking player moved towards the opponent's goal to the east for a distance of \[50\;\; m\] in a straight line during a time of \[t=8 \;\;s\] then the ball bounced back and moved in the opposite direction covering a distance of \[30\;\; m\] during a time of \[10\;\;s\] The average speed during the attack phase, the average speed during the bounce phase, and the average speed for the entire period equal
\[𝑣_1=3.33 m/s\;\;,\;\; 𝑣_2=1.7 m/s\;\;,\;\;𝑣=-4.44 m/s\;\;\;\;\;\;-C\] |
\[𝑣_1=3.33 m/s\;\;,\;\; 𝑣_2=-3 m/s\;\;,\;\;𝑣=4.44 m/s\;\;\;\;\;\;-A\] |
\[𝑣_1=6.25 m/s\;\;,\;\; 𝑣_2=-3 m/s\;\;,\;\;𝑣=1.11 m/s\;\;\;\;\;\;-D\] |
\[𝑣_1=6.25 m/s\;\;,\;\; 𝑣_2=3 m/s\;\;,\;\;𝑣=4.44 m/s\;\;\;\;\;\;-B\] |
Click here to show solution
Choose the correct answer
The graph shows the relationship between velocity and time for a bicycle moving in one dimension
The best graph that shows the relationship between acceleration and time for this motion
Click here to show solution
Choose the correct answer
The graph shows the relationship between
(Position - Time)
for the motion of a tractor
At what moment was the velocity zero and at what moment was the acceleration zero
\[(𝑣=0 →𝑡=10 𝑠)(𝑎=0 →𝑡=35 𝑠)\;\;\;\;\;\;-C\] |
\[ (𝑣=0 →𝑡=20 𝑠)(𝑎=0 →𝑡=20 𝑠)\;\;\;\;\;\;-A\] |
\[ (𝑣=0 →𝑡=20 𝑠)(𝑎=0 →𝑡=30 𝑠) \;\;\;\;\;\;-D\] |
\[ (𝑣=0 →𝑡=35 𝑠)(𝑎=0 →𝑡=20 𝑠) \;\;\;\;\;\;-B\] |
Click here to show solution
Choose the correct answer
The following graph shows the relationship between (Velocity - Time) for a car's motion
Calculate the displacement of the car from second
\[t=15 \;\;s\Rightarrow t=40\;\;s\]
Choose the correct answer
Click here to show solution
Solve the Following Problems
A red car was standing on the side of the road when a blue car passed by moving at a constant speed
\[20 \;\;m/s\] At that moment, the red car started moving with a constant acceleration of An airplane landed on a runway and touched the ground at a speed of
\[50\;\;m/s\] moving with constant deceleration and stopped at a distance of
\[700 \;\;m\] What was its speed after moving on the runway
\[500\;\;m\]
A ball was thrown from the ground surface with an initial speed of
\[20\;\;m/s\] Calculate the speed of the ball at half of the maximum height (neglecting air resistance)
\[g=9.81 m/s^2\]
A balloon is stationary at a height of
\[40\;\;m\] from the ground surface
A ball was dropped to fall freely vertically to the ground
( X ) Determines the position of a body moving on the axis
through the relationship
\[X=9−10 𝑡+2𝑡^2 \] where \[X(m) , t(s) \] Determine the position of the body when it reaches maximum displacement
\[........................................................................................\]
\[........................................................................................\]
\[........................................................................................\]
\[........................................................................................\]
\[........................................................................................\]
Click here to show the solution method
\[3\;\;m/s^2\]
How much time does the red car need to catch up with the blue car?
\[........................................................................................\]
\[........................................................................................\]
\[........................................................................................\]
What is the distance traveled by the red car until it reaches the blue car?
\[........................................................................................\]
\[........................................................................................\]
Click here to show the solution method
\[........................................................................................\]
\[........................................................................................\]
\[........................................................................................\]
\[........................................................................................\]
\[........................................................................................\]
Click here to show the solution method
\[........................................................................................\]
\[........................................................................................\]
\[........................................................................................\]
\[........................................................................................\]
\[........................................................................................\]
Click here to show the solution method
At the same moment the ball was dropped, an arrow was fired from
the ground surface vertically at the ball with a speed of
\[30\;\;m/s\]
At what height will the ball and arrow meet?
\[........................................................................................\]
\[........................................................................................\]
\[........................................................................................\]
\[........................................................................................\]
\[........................................................................................\]
Click here to show the solution method
0 Comments