📄 Print pdf
00971504825082
(11 A ) Question Bank: Motion in Two and Three Dimensions
\[1\star\]
In projectile motion at an angle, the acceleration at maximum height reached by the projectile is:
\[ a=-4.95 \;\; m/s^2\;\;\;\;\;\;-C\]
\[ a=0 \;\; m/s^2\;\;\;\;\;\;-A\]
\[ a=-6.25 \;\; m/s^2\;\;\;\;\;\;-D\]
\[ a=-9.81 \;\; m/s^2\;\;\;\;\;\;-B\]
Click here to show solution
Choose the correct answer
\[2\star \star\]
Ahmed threw a ball with initial velocity
\[\overrightarrow v =( 31 \widehat X + 20 \widehat Y ) \]from a building's surface and it reached the ground after
time
\[t=3.8\;\; s\]
The velocity of the ball upon hitting the ground equals:
\[ 𝑣= 51 \;\;𝑚/𝑠\;\;\;\;\;\;-C\]
\[ 𝑣= 31.4 \;\;𝑚/𝑠 \;\;\;\;\;\;-A\]
\[ 𝑣= 41.3 \;\;𝑚/𝑠\;\;\;\;\;\;-D\]
\[ 𝑣= 35.5 \;\;𝑚/𝑠\;\;\;\;\;\;-B\]
Click here to show solution
Choose the correct answer
\[3\star \star\]
In a golf game, the ball was hit from the ground four times with the same initial velocity but at different angles. The maximum range reached by the ball occurs when hit at angle:
\[𝜃_1=20^0\;\;\;\;\;𝜃_2=30^0\;\;\;\;\;𝜃_3=45^0\;\;\;\;\;𝜃_4=60^0\]
\[ 𝜃=45^0\;\;\;\;\;\;-C\]
\[ 𝜃=20^0\;\;\;\;\;\;-A\]
\[ 𝜃=60^0\;\;\;\;\;\;-D\]
\[ 𝜃=30^0\;\;\;\;\;\;-B\]
Click here to show solution
Choose the correct answer
\[4\star \star\]
In a golf game, the ball was hit from the ground twice with the same initial velocity but at different angles
\[𝜃_1=30^0\;\;\;\;\;𝜃_2=60^0 \]
When comparing the range of the two balls, one of the answers represents the horizontal range of the two balls:
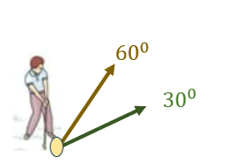
\[ R_2>R_1\;\;\;\;\;\;-C\]
\[ R_1>R_2\;\;\;\;\;\;-A\]
Insufficient data-D
\[ R_1=R_2\;\;\;\;\;\;-B\]
Click here to show solution
Choose the correct answer
\[5\star \star\]
The position equation of an object on the horizontal axis as a function of time
\[X(t)= 3 -6 .t -4. t^2+ t^3 \]
and the position equation of the same object on the vertical axis as a function of time
\[Y(𝑡)=-5.t^2+t^3\]
Then the velocity at which the object moves at the moment \[t=4\;\; s\] equals
\[𝑣= (10 \widehat X , 8 \widehat Y )m/s\;\;\;\;\;\;-C\]
\[ 𝑣= (11 \widehat X , 9 \widehat Y )m/s \;\;\;\;\;\;-A\]
\[𝑣= (16 \widehat X , 9 \widehat Y )m/s\;\;\;\;\;\;-D\]
\[𝑣= (18 \widehat X , 12 \widehat Y )m/s\;\;\;\;\;\;-B\]
Click here to show the solution
Choose the correct answer
\[6\star \star \star\]
A player kicked a ball (projected at an angle) with an initial speed of
\[v_0=45\;\;m/s\] to reach his teammate who is at a distance
\[X=30.6 m\]
Then the angle at which the ball was thrown with the horizontal is
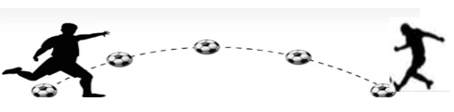
\[𝜃=8.5^0\;\;\;\;\;\;-C\]
\[𝜃=3.1^0\;\;\;\;\;\;-A\]
\[𝜃=4.25^0\;\;\;\;\;\;-D\]
\[𝜃=10.3^0\;\;\;\;\;\;-B\]
Click here to show the solution
Choose the correct answer
\[7\star \star\]
A cannon fired a projectile with an initial horizontal velocity
\[v_0=31 \;\;m/s\] from the top of a building. The projectile reached the ground after
a time of \[t=4\;\;s\]. Then the velocity of the projectile upon hitting the ground equals
\[𝑣=31\;\; 𝑚/𝑠\;\;\;\;\;\;-C\]
\[ 𝑣= 67\;\; 𝑚/𝑠\;\;\;\;\;\;-A\]
\[𝑣= 50\;\; 𝑚/𝑠\;\;\;\;\;\;-D\]
\[𝑣= 43\;\; 𝑚/𝑠\;\;\;\;\;\;-B\]
Click here to show the solution
Choose the correct answer
\[8\star \star \star\]
The horizontal displacement equation of a projectile at a specific location was written as shown below
and at the same moment the vertical displacement of the same body at the same location was written \[ ∆𝑋=36. 𝑡\]\[∆𝑌=48.𝑡−4.9𝑡^2\]
Then the initial velocity at which the body was thrown
\[𝑣_i=45\;\; 𝑚/𝑠\;\;\;\;\;\;-C\]
\[ 𝑣_i= 40\;\; 𝑚/𝑠\;\;\;\;\;\;-A\]
\[𝑣_i= 55\;\; 𝑚/𝑠\;\;\;\;\;\;-D\]
\[𝑣_i=60\;\; 𝑚/𝑠\;\;\;\;\;\;-B\]
Click here to show the solution
Choose the correct answer
\[9\star \star\]
Majid moved east a distance
\[60\;\;m\]
then continued walking in the same direction a distance
\[80\;\;m\]
then changed his direction north and covered a distance
\[50\;\;m\]
then headed west and covered a distance
\[40\;\;m\]
Then the distance and displacement covered equal
\[𝑠=230\;\ m \;\;\;r=127 \;m\;\;\;\;\;\;-C\]
And the displacement makes an angle of 18 degrees north of east
\[𝑠=130\;\ m \;\;\;r=170 \;m\;\;\;\;\;\;-A\]
And the displacement makes an angle of 32 degrees north of east
\[𝑠=230\;\ m \;\;\;r=107.7 \;m\;\;\;\;\;\;-D\]
And the displacement makes an angle of 21.8 degrees north of east
\[𝑠=130\;\ m \;\;\;r=132 \;m\;\;\;\;\;\;-B\]
And the displacement makes an angle of 15 degrees north of east
Click here to show the solution
Choose the correct answer
\[10\star \star\]
An archer stands on a hill 30 m above the ground and shoots an arrow at a 35-degree angle. The arrow reached a maximum height of 52 m above the ground. The initial velocity with which the arrow was launched equals:
\[𝑣_0=36.26 \;\;m/s\;\;\;\;\;\;-C\]
\[ 𝑣_0=18.67 \;\;m/s\;\;\;\;\;\;-A\]
\[𝑣_0=21.24 \;\;m/s\;\;\;\;\;\;-D\]
\[𝑣_0=25.36\;\;m/s\;\;\;\;\;\;-B\]
Click here to show solution
Choose the correct answer
\[11\star\]
Ahmed kicked a ball from the ground with a speed of 20 m/s at a 15-degree angle above the horizontal. The maximum height the ball reaches is:
\[𝐻=1.36\;\; m\;\;\;\;\;\;-C\]
\[𝐻=0.98\;\; m\;\;\;\;\;\;-A\]
\[𝐻=1.75\;\; m\;\;\;\;\;\;-D\]
\[𝐻=2.11\;\; m\;\;\;\;\;\;-B\]
Click here to show solution
Choose the correct answer
\[12\star\]
A ball was thrown with an initial velocity at an angle θ above the horizontal from the top of a cliff as shown in the figure below. Which of the following graphs represents the relationship between vertical velocity and time?
Click here to show solution
Choose the correct answer
\[13\star\]
In projectile motion at an angle, the correct representation of the velocity vector and acceleration vector at maximum height is expressed by which figure?
Click here to show solution
Choose the correct answer
\[14\star \star\]
A catapult throws a stone with an initial speed of 40 m/s at a 30-degree angle above the horizontal. The speed of the stone at a height of 8 m equals:
\[𝑣=45.6 \;\;m/s\;\;\;\;\;\;-C\]
\[𝑣=28.5 \;\;m/s\;\;\;\;\;\;-A\]
\[𝑣=37.9 \;\;m/s\;\;\;\;\;\;-D\]
\[𝑣=22.3 \;\;m/s\;\;\;\;\;\;-B\]
Click here to show solution
Choose the correct answer
\[15\star\]
A ball was kicked with an initial velocity of \[\overrightarrow v =( 12 \widehat X + 6 \widehat Y ) \]. The magnitude of the initial velocity and the angle it makes with the horizontal axis equals:
\[𝑣_0 =20 \;m/s \;\; 𝜃=21.3^0 \;\;\;\;\;\;-C\]
\[𝑣_0 =20 \;m/s \;\; 𝜃=26.5^0 \;\;\;\;\;\;-A\]
\[𝑣_0 =13.4 \;m/s \;\; 𝜃=21.3^0 \;\;\;\;\;\;-D\]
\[𝑣_0 =13.4 \;m/s \;\; 𝜃=26.5^0 \;\;\;\;\;\;-B\]
Click here to show solution
Choose the correct answer
\[16\star \star\]
A boat is moving in a river heading east at speed
\[v=8\;\;m/s\] while the river flows north at speed \[v=6m/s\]. The boat's speed and direction of motion relative to an observer standing on the shore equals
\[𝑣_{Be} =10 \;m/s \;\; 𝜃=36.8^0 \;\;\;\;\;\;-C\]
\[𝑣_{Be} =10 \;m/s \;\; 𝜃=18.6^0 \;\;\;\;\;\;-A\]
\[𝑣_{Be} =14 \;m/s \;\; 𝜃=18.6^0 \;\;\;\;\;\;-D\]
\[𝑣_{Be} =14 \;m/s \;\; 𝜃=36.8^0 \;\;\;\;\;\;-B\]
Click here to show solution
Choose the correct answer
Solve the following problems
\[1\star\]
In a movie scene, actor Jackie Chan jumped from a building with height above ground
\[30 \;\;m\] to
another building with height above ground \[26\;\;m\] with initial velocity and angle \[v_0=? \;\;\;\;\;\;𝜃=13^0\] and reached
the second building which is
\[5\;\;m\] away from the first building. What is the minimum initial velocity needed for safety?
\[.....................................\;\;\;\;............................................\]
\[.....................................\;\;\;\;............................................\]
\[.....................................\;\;\;\;............................................\]
\[.....................................\;\;\;\;............................................\]
\[.....................................\;\;\;\;............................................\]
\[.....................................\;\;\;\;............................................\]
Click here to show solution
\[2\star\]
A ball was thrown horizontally from a building with height above ground
\[20\;\;m\] and hit the ground at
\[30/;\;m\]
from the base of the building
How long did the ball remain in the air?
\[.....................................\;\;\;\;............................................\]
\[.....................................\;\;\;\;............................................\]
Calculate the velocity at which the ball was thrown
\[.....................................\;\;\;\;............................................\]
\[.....................................\;\;\;\;............................................\]
Calculate the ball's velocity upon hitting the ground
\[.....................................\;\;\;\;............................................\]
\[.....................................\;\;\;\;............................................\]
Click here to show solution
\[3\star\]
An archer shot an arrow at a target 80 meters away
where the target is at the same height as the arrow's launch point
Calculate the angle at which the arrow must be launched to hit the center of the target if its initial velocity is
\[v_0=30\;\;m/s\]
\[.....................................\;\;\;\;............................................\]
\[.....................................\;\;\;\;............................................\]
\[.....................................\;\;\;\;............................................\]
\[.....................................\;\;\;\;............................................\]
\[.....................................\;\;\;\;............................................\]
\[.....................................\;\;\;\;............................................\]
A horizontal crossbar was found resting on supports at the midpoint between the archer and the target at height
\[3.5 \;\;m\] above the arrow's launch height. Will the arrow pass above or below the crossbar?
\[.....................................\;\;\;\;............................................\]
\[.....................................\;\;\;\;............................................\]
\[.....................................\;\;\;\;............................................\]
Click here to show solution
(11 A ) Question Bank: Motion in Two and Three Dimensions |
In projectile motion at an angle, the acceleration at maximum height reached by the projectile is:
\[ a=-4.95 \;\; m/s^2\;\;\;\;\;\;-C\] |
\[ a=0 \;\; m/s^2\;\;\;\;\;\;-A\] |
\[ a=-6.25 \;\; m/s^2\;\;\;\;\;\;-D\] |
\[ a=-9.81 \;\; m/s^2\;\;\;\;\;\;-B\] |
Click here to show solution
Choose the correct answer
Ahmed threw a ball with initial velocity
\[\overrightarrow v =( 31 \widehat X + 20 \widehat Y ) \]from a building's surface and it reached the ground after
time
\[t=3.8\;\; s\]
The velocity of the ball upon hitting the ground equals:
\[ 𝑣= 51 \;\;𝑚/𝑠\;\;\;\;\;\;-C\] |
\[ 𝑣= 31.4 \;\;𝑚/𝑠 \;\;\;\;\;\;-A\] |
\[ 𝑣= 41.3 \;\;𝑚/𝑠\;\;\;\;\;\;-D\] |
\[ 𝑣= 35.5 \;\;𝑚/𝑠\;\;\;\;\;\;-B\] |
Click here to show solution
Choose the correct answer
In a golf game, the ball was hit from the ground four times with the same initial velocity but at different angles. The maximum range reached by the ball occurs when hit at angle:
\[𝜃_1=20^0\;\;\;\;\;𝜃_2=30^0\;\;\;\;\;𝜃_3=45^0\;\;\;\;\;𝜃_4=60^0\]
\[ 𝜃=45^0\;\;\;\;\;\;-C\] |
\[ 𝜃=20^0\;\;\;\;\;\;-A\] |
\[ 𝜃=60^0\;\;\;\;\;\;-D\] |
\[ 𝜃=30^0\;\;\;\;\;\;-B\] |
Click here to show solution
Choose the correct answer
In a golf game, the ball was hit from the ground twice with the same initial velocity but at different angles
\[𝜃_1=30^0\;\;\;\;\;𝜃_2=60^0 \]
When comparing the range of the two balls, one of the answers represents the horizontal range of the two balls:
\[ R_2>R_1\;\;\;\;\;\;-C\] |
\[ R_1>R_2\;\;\;\;\;\;-A\] |
Insufficient data-D |
\[ R_1=R_2\;\;\;\;\;\;-B\] |
Click here to show solution
Choose the correct answer
The position equation of an object on the horizontal axis as a function of time \[X(t)= 3 -6 .t -4. t^2+ t^3 \] and the position equation of the same object on the vertical axis as a function of time \[Y(𝑡)=-5.t^2+t^3\] Then the velocity at which the object moves at the moment \[t=4\;\; s\] equals
\[𝑣= (10 \widehat X , 8 \widehat Y )m/s\;\;\;\;\;\;-C\] |
\[ 𝑣= (11 \widehat X , 9 \widehat Y )m/s \;\;\;\;\;\;-A\] |
\[𝑣= (16 \widehat X , 9 \widehat Y )m/s\;\;\;\;\;\;-D\] |
\[𝑣= (18 \widehat X , 12 \widehat Y )m/s\;\;\;\;\;\;-B\] |
Click here to show the solution
Choose the correct answer
A player kicked a ball (projected at an angle) with an initial speed of
\[v_0=45\;\;m/s\] to reach his teammate who is at a distance
\[X=30.6 m\]
Then the angle at which the ball was thrown with the horizontal is
\[𝜃=8.5^0\;\;\;\;\;\;-C\] |
\[𝜃=3.1^0\;\;\;\;\;\;-A\] |
\[𝜃=4.25^0\;\;\;\;\;\;-D\] |
\[𝜃=10.3^0\;\;\;\;\;\;-B\] |
Click here to show the solution
Choose the correct answer
A cannon fired a projectile with an initial horizontal velocity
\[v_0=31 \;\;m/s\] from the top of a building. The projectile reached the ground after
a time of \[t=4\;\;s\]. Then the velocity of the projectile upon hitting the ground equals
\[𝑣=31\;\; 𝑚/𝑠\;\;\;\;\;\;-C\] |
\[ 𝑣= 67\;\; 𝑚/𝑠\;\;\;\;\;\;-A\] |
\[𝑣= 50\;\; 𝑚/𝑠\;\;\;\;\;\;-D\] |
\[𝑣= 43\;\; 𝑚/𝑠\;\;\;\;\;\;-B\] |
Click here to show the solution
Choose the correct answer
The horizontal displacement equation of a projectile at a specific location was written as shown below and at the same moment the vertical displacement of the same body at the same location was written \[ ∆𝑋=36. 𝑡\]\[∆𝑌=48.𝑡−4.9𝑡^2\] Then the initial velocity at which the body was thrown
\[𝑣_i=45\;\; 𝑚/𝑠\;\;\;\;\;\;-C\] |
\[ 𝑣_i= 40\;\; 𝑚/𝑠\;\;\;\;\;\;-A\] |
\[𝑣_i= 55\;\; 𝑚/𝑠\;\;\;\;\;\;-D\] |
\[𝑣_i=60\;\; 𝑚/𝑠\;\;\;\;\;\;-B\] |
Click here to show the solution
Choose the correct answer
Majid moved east a distance
\[60\;\;m\]
then continued walking in the same direction a distance
\[80\;\;m\]
then changed his direction north and covered a distance
\[50\;\;m\]
then headed west and covered a distance
\[40\;\;m\]
Then the distance and displacement covered equal
\[𝑠=230\;\ m \;\;\;r=127 \;m\;\;\;\;\;\;-C\] And the displacement makes an angle of 18 degrees north of east |
\[𝑠=130\;\ m \;\;\;r=170 \;m\;\;\;\;\;\;-A\] And the displacement makes an angle of 32 degrees north of east |
\[𝑠=230\;\ m \;\;\;r=107.7 \;m\;\;\;\;\;\;-D\] And the displacement makes an angle of 21.8 degrees north of east |
\[𝑠=130\;\ m \;\;\;r=132 \;m\;\;\;\;\;\;-B\] And the displacement makes an angle of 15 degrees north of east |
Click here to show the solution
Choose the correct answer
An archer stands on a hill 30 m above the ground and shoots an arrow at a 35-degree angle. The arrow reached a maximum height of 52 m above the ground. The initial velocity with which the arrow was launched equals:
\[𝑣_0=36.26 \;\;m/s\;\;\;\;\;\;-C\] |
\[ 𝑣_0=18.67 \;\;m/s\;\;\;\;\;\;-A\] |
\[𝑣_0=21.24 \;\;m/s\;\;\;\;\;\;-D\] |
\[𝑣_0=25.36\;\;m/s\;\;\;\;\;\;-B\] |
Click here to show solution
Choose the correct answer
Ahmed kicked a ball from the ground with a speed of 20 m/s at a 15-degree angle above the horizontal. The maximum height the ball reaches is:
\[𝐻=1.36\;\; m\;\;\;\;\;\;-C\] |
\[𝐻=0.98\;\; m\;\;\;\;\;\;-A\] |
\[𝐻=1.75\;\; m\;\;\;\;\;\;-D\] |
\[𝐻=2.11\;\; m\;\;\;\;\;\;-B\] |
Click here to show solution
Choose the correct answer
A ball was thrown with an initial velocity at an angle θ above the horizontal from the top of a cliff as shown in the figure below. Which of the following graphs represents the relationship between vertical velocity and time?
Click here to show solution
Choose the correct answer
In projectile motion at an angle, the correct representation of the velocity vector and acceleration vector at maximum height is expressed by which figure?
Click here to show solution
Choose the correct answer
A catapult throws a stone with an initial speed of 40 m/s at a 30-degree angle above the horizontal. The speed of the stone at a height of 8 m equals:
\[𝑣=45.6 \;\;m/s\;\;\;\;\;\;-C\] |
\[𝑣=28.5 \;\;m/s\;\;\;\;\;\;-A\] |
\[𝑣=37.9 \;\;m/s\;\;\;\;\;\;-D\] |
\[𝑣=22.3 \;\;m/s\;\;\;\;\;\;-B\] |
Click here to show solution
Choose the correct answer
A ball was kicked with an initial velocity of \[\overrightarrow v =( 12 \widehat X + 6 \widehat Y ) \]. The magnitude of the initial velocity and the angle it makes with the horizontal axis equals:
\[𝑣_0 =20 \;m/s \;\; 𝜃=21.3^0 \;\;\;\;\;\;-C\] |
\[𝑣_0 =20 \;m/s \;\; 𝜃=26.5^0 \;\;\;\;\;\;-A\] |
\[𝑣_0 =13.4 \;m/s \;\; 𝜃=21.3^0 \;\;\;\;\;\;-D\] |
\[𝑣_0 =13.4 \;m/s \;\; 𝜃=26.5^0 \;\;\;\;\;\;-B\] |
Click here to show solution
Choose the correct answer
A boat is moving in a river heading east at speed
\[v=8\;\;m/s\] while the river flows north at speed \[v=6m/s\]. The boat's speed and direction of motion relative to an observer standing on the shore equals
\[𝑣_{Be} =10 \;m/s \;\; 𝜃=36.8^0 \;\;\;\;\;\;-C\] |
\[𝑣_{Be} =10 \;m/s \;\; 𝜃=18.6^0 \;\;\;\;\;\;-A\] |
\[𝑣_{Be} =14 \;m/s \;\; 𝜃=18.6^0 \;\;\;\;\;\;-D\] |
\[𝑣_{Be} =14 \;m/s \;\; 𝜃=36.8^0 \;\;\;\;\;\;-B\] |
Click here to show solution
Choose the correct answer
Solve the following problems
In a movie scene, actor Jackie Chan jumped from a building with height above ground \[30 \;\;m\] to another building with height above ground \[26\;\;m\] with initial velocity and angle \[v_0=? \;\;\;\;\;\;𝜃=13^0\] and reached the second building which is \[5\;\;m\] away from the first building. What is the minimum initial velocity needed for safety?
Click here to show solution
A ball was thrown horizontally from a building with height above ground \[20\;\;m\] and hit the ground at \[30/;\;m\] from the base of the building How long did the ball remain in the air?
Click here to show solution
An archer shot an arrow at a target 80 meters away
where the target is at the same height as the arrow's launch point
Calculate the angle at which the arrow must be launched to hit the center of the target if its initial velocity is
\[v_0=30\;\;m/s\]
\[.....................................\;\;\;\;............................................\]
\[.....................................\;\;\;\;............................................\]
\[.....................................\;\;\;\;............................................\]
\[.....................................\;\;\;\;............................................\]
\[.....................................\;\;\;\;............................................\]
\[.....................................\;\;\;\;............................................\]
A horizontal crossbar was found resting on supports at the midpoint between the archer and the target at height
\[3.5 \;\;m\] above the arrow's launch height. Will the arrow pass above or below the crossbar?
\[.....................................\;\;\;\;............................................\]
\[.....................................\;\;\;\;............................................\]
\[.....................................\;\;\;\;............................................\]
Click here to show solution
0 Comments