📄 Print pdf
00971504825082
Sound
Click here to show learning outcomes
Click here to view the learning outcomes
Sound |
Click here to show learning outcomes
Click here to view the learning outcomes
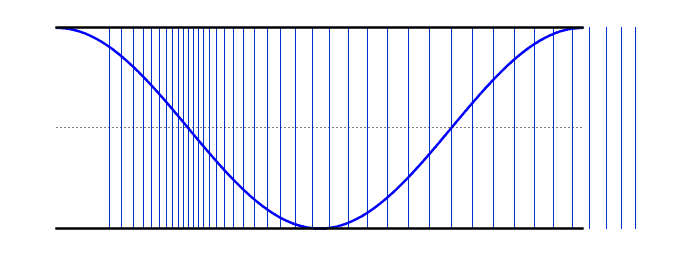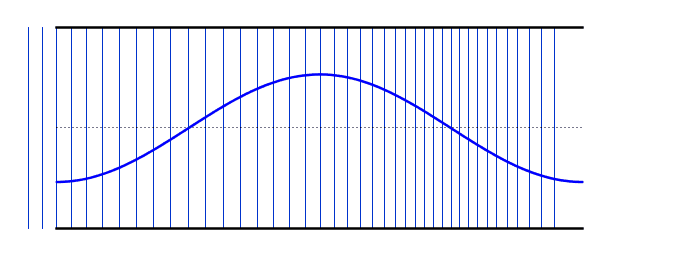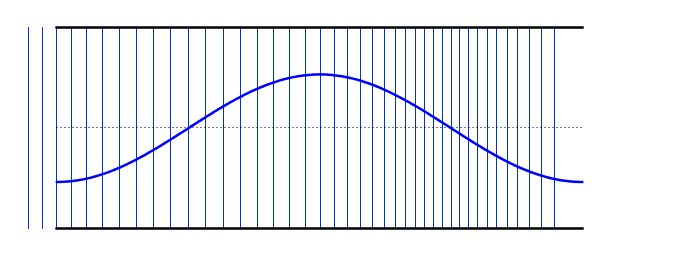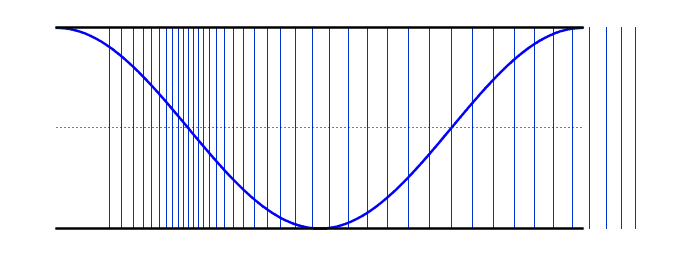
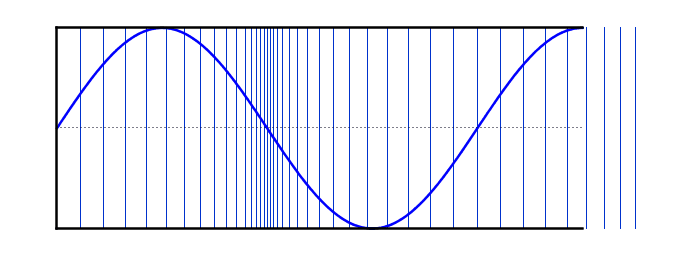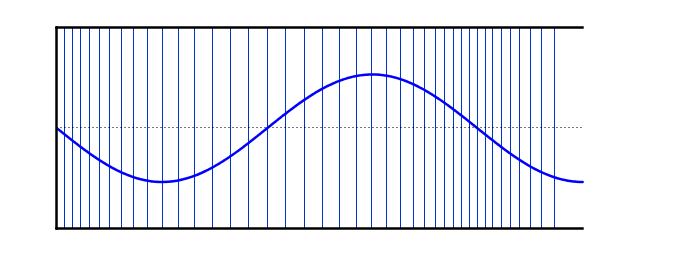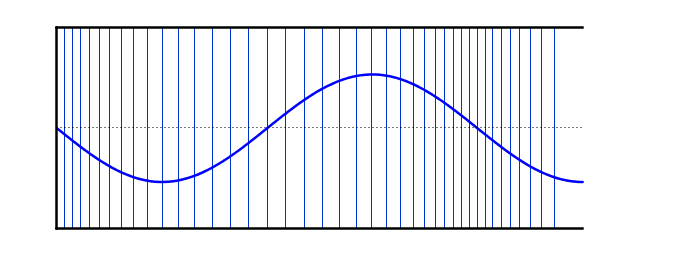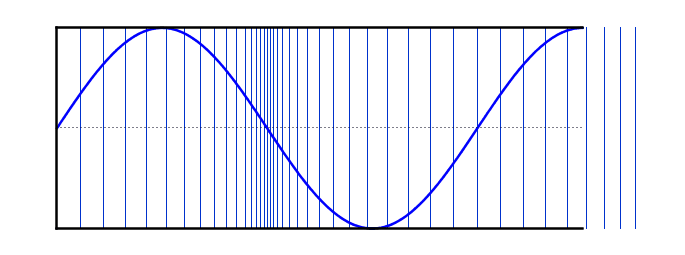
Sound: is a form of energy
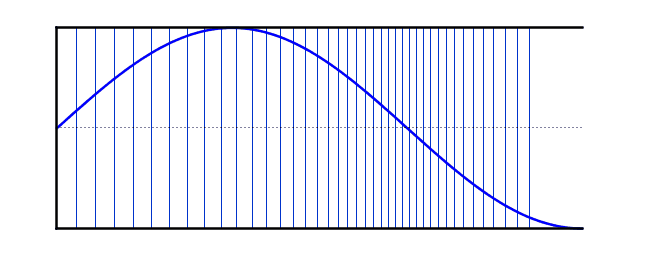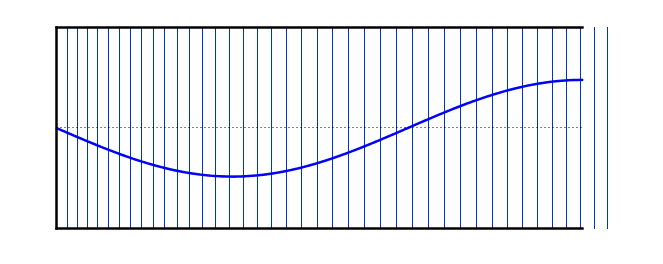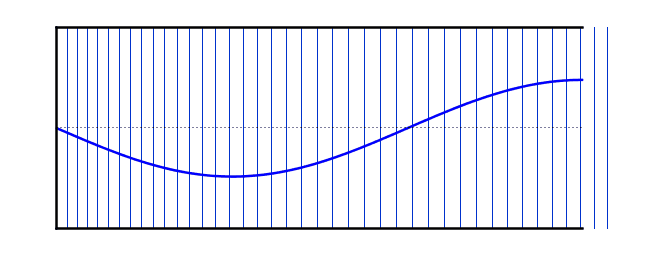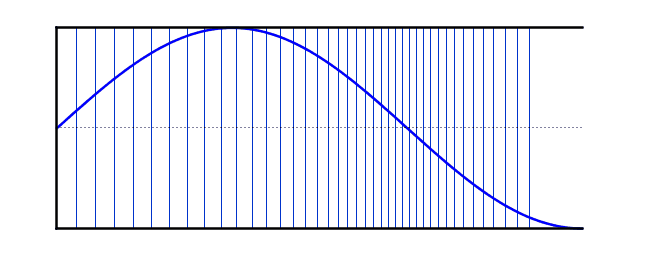
that vibrates and travels in waves
Speaker: When the paper cone moves forward, it pushes the molecules together. This creates a high-pressure area
called the compressed part of the sound wave
When the paper cone moves in the opposite direction, it creates a low-pressure area
resulting in the formation of the rarefaction part of the wave
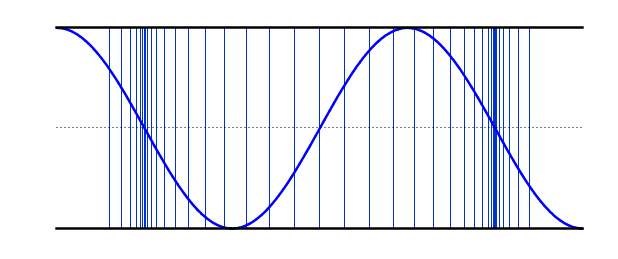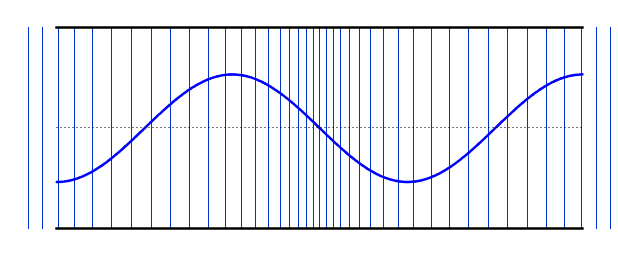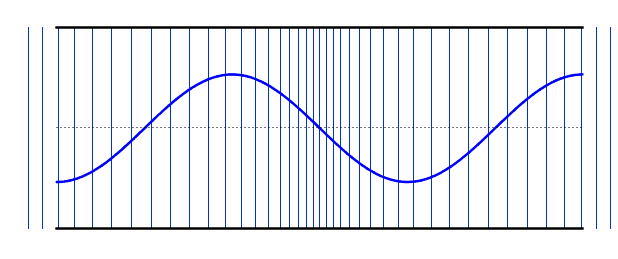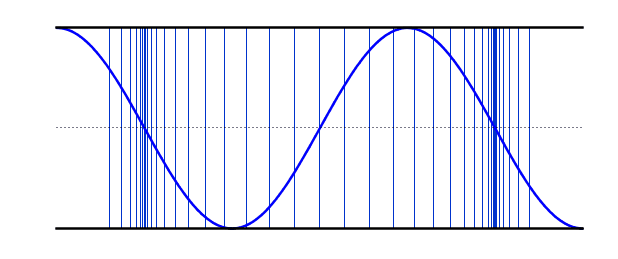
Simulation of Air Molecule Vibrations Due to Sound
This simulation shows how sound waves are produced by the vibration of air molecules.
When the simulation is running, you will see air molecules (blue dots) vibrating around their original positions (gray lines) without moving from their place.
The areas where molecules come closer together are called "compression" and the areas where they move apart are called "rarefaction".
Sound is a mechanical wave because it needs a medium to travel through
Sound is a longitudinal wave because the vibration of molecules is parallel to the propagation of vibration
We call the number of waves emitted by a source per second the frequency of the wave
We call the convergence of air molecules compression
We call the divergence of air molecules rarefaction
We call the distance between two consecutive compressions or two consecutive rarefactions the wavelength
We call the maximum displacement from the equilibrium position of air molecules the amplitude of the wave
Sound wave speed is the distance the wave travels per unit time \[v=\frac {X}{t}= \frac {𝝀}{T}=𝝀.f \;\;\;\;\; (\frac {m}{s})\] The speed of the wave changes with the type of medium or the temperature of the medium
Speed of sound in various media |
m/s |
Medium at a specific temperature |
331 |
Air at 0°C |
334 |
Air at 20°C |
965 |
Helium at 0°C |
1497 |
Water at 25°C |
1535 |
Seawater at 25°C |
4760 |
Copper at 20°C |
4994 |
Iron at 20°C |
By reviewing the table data, explain
Why does the speed of sound in air change with temperature? \[............................\;\;\;\;\;\;..................................\] \[............................\;\;\;\;\;\;..................................\]
Why is the speed of sound in solids greater than in liquids? \[............................\;\;\;\;\;\;..................................\] \[............................\;\;\;\;\;\;..................................\]
Click here to show solution method
The microphone consists of a magnetic field - a coil connected to a thin diaphragm
Sound is compression and rarefaction of air molecules when we speak in front of a thin diaphragm
The diaphragm vibrates causing the coil inside the field to vibrate
resulting in induced alternating current
When sound occurs, it enters the outer ear
Sound waves enter the outer ear and travel through a narrow passage called the ear canal
and reach the eardrum. The eardrum vibrates due to incoming sound waves and sends these vibrations to three bones
These bones are called the hammer, anvil, and stirrup
The bones in the middle ear amplify or increase the sound vibrations and send them to the cochlea
The vibrations cause fluid inside the cochlea to ripple
which transmits them to sensory cells
It is a characteristic of sound that distinguishes between high-pitched and low-pitched sounds
The higher the frequency of the sound, the more sharp and high-pitched it becomes
Humans can hear sounds with frequencies ranging from \[20\; HZ\;\;\;\;\; \iff \;\;\; 16000\; Hz \]while animals can hear frequencies that humans cannot
It is a characteristic of sound distinguished by the ear
defined as the energy carried by sound waves per unit area
It depends on the amplitude of the wave and distance from the source and other factors affecting sound intensity
To reduce these factors, sound intensity level is used which is measured in decibels
Humans can hear sounds with intensity levels from \[0\; dB\;\;\;\;\; \iff \;\;\; 120\; dB \]and when exceeding 120 decibels, pain is felt
This phenomenon occurs when the sound source moves towards or away from the listener
and occurs when the listener moves towards or away from the sound source
The frequency of sound reaching the listener due to the movement of either the source or listener or both is calculated by the relationship
\[f_d=f_s\frac {v-v_d}{v-v_s}\]
When applying the Doppler effect, we must determine a positive direction which is from the source to the observerThe speed of sound is always positive because sound waves are spherical waves propagating in all directions
While the speed of the source and the speed of the observer take positive and negative signs according to the assumed positive direction
Observer moving away from the source |
Observer moving towards the source |
Stationary observer |
\[f_d=f_s\frac {v-v_d}{v-v_s}\] |
\[f_d=f_s\frac {v-v_d}{v}\] |
\[f_d=f_s\frac {v+v_d}{v}\] |
\[f_s=f_d\] |
Stationary source |
\[f_d=f_s\frac {v-v_d}{v-v_s}\] |
\[f_d=f_s\frac {v+v_d}{v-v_s}\] |
\[f_d=f_s\frac {v}{v-v_s}\] |
Source moving towards the observer |
\[f_d=f_s\frac {v-v_d}{v+v_s}\] |
\[f_d=f_s\frac {v+v_d}{v+v_s}\] |
\[f_d=f_s\frac {v}{v+v_s}\] |
Source moving away from the observer |
This simulation verifies the results in the previous table
A train emits sound with a frequency of 250 Hz
( 40 m/s ) moving at a speed of
( 344 m/s ) in still air on a day when the speed of sound is
What frequencies are observed by a person standing by the tracks as the train approaches \[f_d=f_s\frac {v}{v-v_s}\] \[f_d=250 ×\frac {344}{344-40}=282.9 Hz \] What frequencies are observed by the person standing by the tracks after the train passes \[f_d=f_s\frac {v}{v+v_s}\] \[f_d=250 ×\frac {344}{344+40}=223.9 Hz \]
0 Comments