📄 Print pdf
00971504825082
Vibrations and Waves


Periodic Motion
Periodic Motion: Any motion that repeats itself, like the motions shown in the previous images
Vibrational motion is a periodic motion where an object oscillates around an equilibrium position
We will study a special case of vibrational motion called Simple Harmonic Motion
Simple Harmonic Motion:
A type of vibrational motion in a straight line around an equilibrium position where the restoring force is directly proportional to the displacement of the object and opposite in direction
Some characteristics of Simple Harmonic Motion Amplitude
The maximum displacement of the object from the equilibrium position
\[A\]

Frequency
The number of complete oscillations per second
\[f\]
Period is the time required to complete one full cycle
\[T\]

Hooke's Law
Hooke's Law is the law of elasticity discovered by English scientist Robert Hooke in 1660,
which states that for relatively small deformations of an object,
the displacement or size of the deformation is directly proportional to the deforming force or compression,
and under these conditions the object returns to its original shape and size when the force is removed,
The elastic behavior of solids can be explained by Hooke's Law: the deformation of molecules composed of atoms or ions
is directly proportional to the force causing this displacement, and opposite in direction. Mathematically, Hooke's Law is expressed as:
F = - kx
Hooke's Law Simulation Experiment
Hooke's Law Simulation Experiment
Hooke's Law: Force = Spring Constant × Displacement (F = kx)
Mass (grams)
Force (Newton)
Extension (cm)
Hooke's Constant (N/m)
-
-
-
In this experiment we will study the harmonic motion of an object
and determine the restoring force, displacement, kinetic energy and potential energy of an object oscillating around the equilibrium position
Short Quiz: Simple Harmonic Motion
Physics Short Quiz
Simple Harmonic Motion
The Pendulum
Simple Pendulum: A weight at the end of a weightless, inextensible string
with the other end fixed

Restoring Force \[F= - mg .sin (𝜃)\]
Because the string tension is perpendicular to the direction of motion, and the restoring force is negative because the force component is always opposite to the displacement
We consider the pendulum motion as simple harmonic motion if the pendulum is displaced by an angle less than 15 degrees
In this simulation we will study the factors affecting the period of a pendulum moving in simple harmonic motion
\[T = 2𝜋\sqrt{\frac{L}{g}}\]
Pendulum Period Experiment
Pendulum Period Simulation Experiment
Trial Number
Angle (degrees)
Pendulum Length (m)
Time for 10 oscillations (s)
Time for one oscillation (s)
1
10
2
10
3
10
4
10
5
10
Pendulum Length vs Period Relationship
Period Squared vs Length Relationship
Mechanical Waves
Wave: A disturbance that transfers energy through matter or space without transferring matter
Medium - The matter through which the wave travels
Mechanical Waves: Waves that require a physical medium to travel through. Example - Sound waves. Sound waves cannot travel through a vacuum.
When a mechanical wave moves through a physical medium, the particles in the medium oscillate with simple harmonic motion.

Simple Harmonic Motion
The blue ball above is in simple harmonic motion. Imagine this ball represents a particle in a solid material. If this particle is connected to other nearby particles, its motion would affect the motion of surrounding particles.

Transverse Wave
In the diagram above, the motion of the leftmost particle causes the adjacent particle to oscillate.
This oscillation is passed down through the entire chain of particles. Notice that the particles vibrate up and down (vertically)
, while the wave itself moves from left to right (horizontally). This specific type of wave motion is called a transverse wave
.
Transverse Wave - A wave in which the particles of the medium move perpendicular to the direction of wave motion.
Waves can also move through matter when the particles of the medium vibrate back and forth in the direction of wave motion. This type of wave is called a longitudinal wave.
Longitudinal Waves - A wave in which the particles of the medium move parallel to the direction of wave motion.
Longitudinal Waves
In the longitudinal wave above, the leftmost particle vibrates horizontally with simple harmonic motion
, causing the particles to its right to also vibrate with simple harmonic motion
. The wave energy is transferred horizontally to the right.
Transverse mechanical waves can only move through solids, while longitudinal waves can move through solids, liquids and gases.

Surface Waves
Surface Waves:Longitudinal waves originate in the depths of oceans.
While water particles on the surface follow a circular path.
. Sometimes parallel to the wave motion and sometimes perpendicular to the wave motion
Wave Properties and Terminology
Waves have properties closely related to the properties of particle vibrations. The wave period, frequency, and amplitude are defined in the same way as particle oscillations and their frequency and amplitude:
Period - The time required to complete one full vibration. (SI unit: second)
Frequency - The number of vibrations per second. (SI unit: Hertz or inverse second)
Amplitude - The maximum displacement from the equilibrium position. (SI unit: meter)
Wavelength - The distance from one crest to another (or between any two consecutive points in phase). (SI unit: meter)
To explore some properties of transverse and longitudinal waves. Adjust the amplitude and frequency sliders and observe how the waves are affected. Click the "Play" button to start the wave motion. Note that the entire transverse wave has a single equilibrium line, while in longitudinal waves, each particle in the medium has its own equilibrium position.
The speed of a wave depends on the medium through which it travels, not on its frequency or wavelength.
The frequency of a wave is determined by the source that produces the wave - it does not depend on the medium through which the wave travels.
The wavelength of a wave depends on both the speed and frequency of the wave:
\[λ=\frac{v}{f}\]
Graphical Representation of Waves
Wave Behavior
Waves at Boundaries
When a wave reaches a boundary, which is a point where the medium changes, i.e., when it moves to another medium, three things happen. Part of the wave is transmitted to the new medium, some of the wave is reflected back into the original medium, and some of the wave's energy is absorbed. When the new medium is denser, the wave inverts upon reflection (fixed barrier), and when it is less dense, it reflects in the same direction (free barrier)


The animation above shows the entire wave pulse being reflected back into the original medium. In reality, some of the wave pulse's energy would be transmitted to the new medium, and the reflected pulse would have a smaller amplitude (less energy) than the original pulse. Also note that the speed of the reflected wave pulse is the same as the speed of the incident wave pulse. The speed depends on the medium, and the reflected pulse is still in the original medium, so it has the same speed as the incident pulse.
Use the simulation below to explore and think in more detail. It allows you to see how the incoming and reflected pulses combine to form the actual visible pulse on the string.
Constructive and Destructive Interference
When two or more waves interfere in the same medium at the same time, it is referred to as wave interference. The process of interference is easier to understand by observing interfering wave pulses. Use the simulation below to explore the interference of wave pulses. Experiment with waves of different widths and heights, including negative height pulses interfering with positive height pulses.
Note that the wave pulses do not bounce off each other; instead, they pass directly through each other and continue on their way as if nothing happened. This is known as the (principle of independence), and the effect is only visible when they interfere. When two pulses interfere, the resulting wave is the algebraic sum of the two pulses. This is known as the (superposition principle). The superposition principle can be defined as follows: the displacement of the medium from its equilibrium position when multiple waves interfere is equal to the algebraic sum of the displacements of the individual waves.
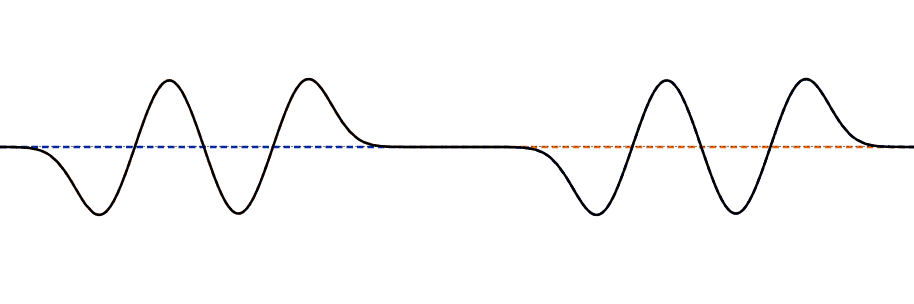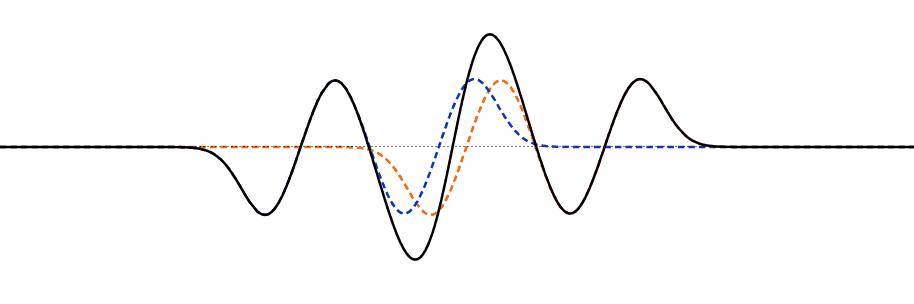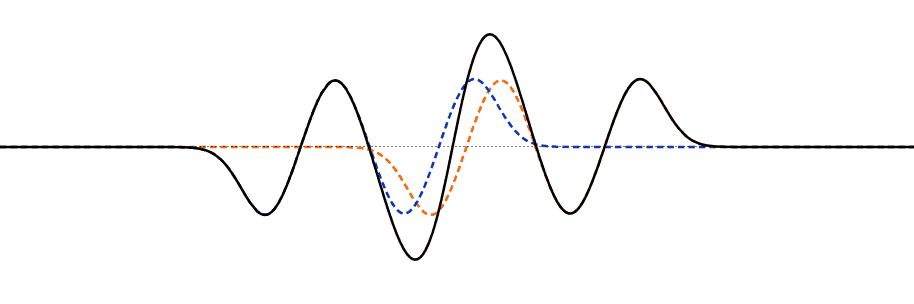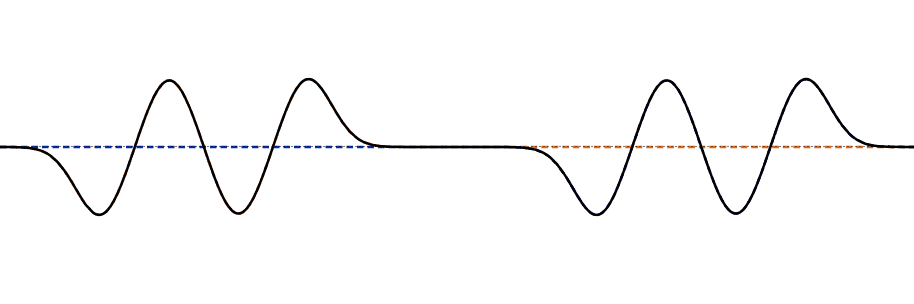
Interference of Multiple Pulses
When multiple pulses interfere, the superposition principle and the principle of independence are applied. The colored dotted lines in the animation show the original shape of the pulses, while the black line shows the actual appearance we see, which is the sum of the original pulses.
Many different interference patterns can appear when two waves interfere. Here are some examples.
In the simulation above, the blue and red waves are moving in the same direction in the same medium (and thus have the same speed). The purple wave at the bottom shows the sum of the blue and red waves. Use the checkbox to see the red and blue waves superimposed on each other. Use the play button in the lower left corner to start the animation. By default, the red and blue waves have the same wavelength and are "in phase". When transverse waves are in phase, they match crest to crest. The sum of the two waves has twice the amplitude of either of the original waves. This is called constructive interference. Use the slider to change the phase of the blue wave. Watch how their sum becomes smaller as the phase difference increases. It is possible for destructive interference to occur, where the waves completely cancel each other out.
Now set the two wavelengths to very different values, for example, try 1.5 for one and 2.5 for the other. Their sum now appears alongside each of the individual waves. This can lead to very complex wave combinations.
When two waves move in the same medium but in opposite directions, different interference patterns form. If two waves moving in opposite directions have the same wavelength, the interference pattern is known as a standing wave
In the simulation shown above, the red and blue waves are moving in the same medium but in opposite directions. When the two waves have different wavelengths, their sum is a complex traveling wave. Now set both wavelengths to the same value (this can also be done by clicking the Show Standing Wave button). Their sum is a special type of wave interference known as a standing wave. A standing wave is called so because it does not move in the direction of either wave. Some points on the standing wave do not move at all; these points are called nodes. The points on the standing wave that undergo the maximum displacement are called antinodes. Use the checkbox to observe the nodes and antinodes.
Standing Waves
When a standing wave forms on a string, there is always a node at each end. This is also known as the first harmonic. The first harmonic: the length of the string is equal to half the wavelength of the standing wave, because the distance from one node to the next is half a wavelength. The frequency of the first standing wave is called the fundamental frequency.
For the first harmonic, the length of the string is equal to half the wavelength of the standing wave, because the distance from a node to the nearest next node is half a wavelength. The frequency of the first standing wave is called the fundamental frequency.
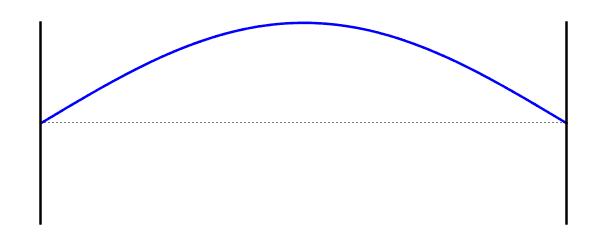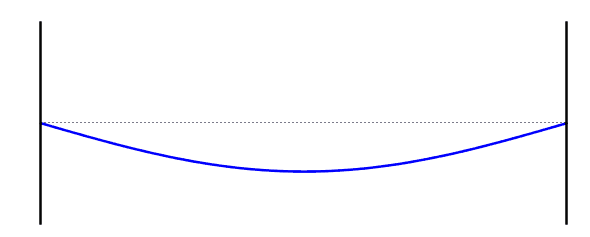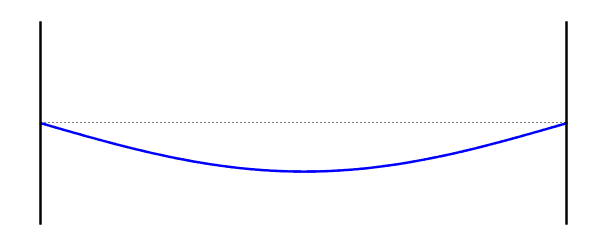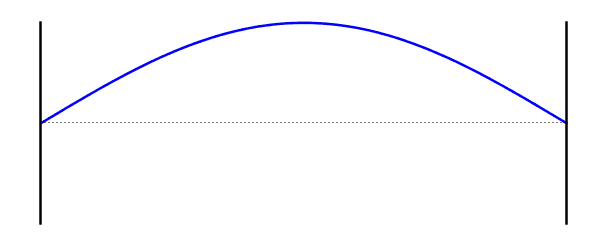
Fundamental Frequency (First Standing Wave)
\[f = f_0 \]\[L =\frac{λ}{2}\]\[λ = 2L\]
There are many other vibration modes for a string fixed at both ends. Each mode is called a harmonic. In the second harmonic, the standing wave consists of two parts. The wavelength is half the fundamental wavelength, and thus the frequency is twice the fundamental frequency.

Second Harmonic Wave
\[f = 2f_0\] \[L = λ\] \[λ = L\]
In the third harmonic, the standing wave consists of three parts. The wavelength is one-third of the fundamental wavelength, and thus the frequency is three times the fundamental frequency.

Third Harmonic Wave
\[f = 3f_0\] \[L = \frac{3λ}{2}\] \[λ = \frac{2L}{3}\]
Waves in Two Dimensions
Think of a pebble dropped into a pond. The water is pushed down and then bounces back up. This causes concentric circles to radiate outward, as shown in this drawing. The rings form as the water level rises and falls.

The white lines are called wavefronts, and the black lines represent the trough. Each ring is a set of points reached by the vibration at the same time period.
We call the distance between one wavefront and the next the wavelength.
Or the distance between two consecutive troughs is the wavelength.
The wave propagates in all directions, and the direction of wave propagation is always perpendicular to the wavefront.
Wave Reflection in Two Dimensions
When mechanical waves hit a barrier, at least part of the wave energy is reflected back into the medium from which it came. You experience this every day.
When a wave hits an obstacle or reaches the end of the medium it is traveling through,
part of the wave is reflected back into the original medium. It is reflected back at an angle equal to the angle of incidence. These angles are called the angle of incidence and the angle of reflection.
The normal line, incident and reflected rays, and the angles of incidence and reflection are shown in this simulation. The law of reflection states that the angle of incidence is equal to the angle of reflection.
The rules of reflection apply, and this is what happens when water waves bounce off the side of a pond.
Wave Refraction in Two Dimensions
How does a wave behave when it passes from one medium to another at a non-perpendicular angle to the interface between the two media?
Wave refraction: is the bending of waves as they pass from one medium to another. When a wave hits the surface of a different medium, some of it is reflected, while some bends and changes direction as it passes through the medium.
A light ray passes from air into water. Note that water has a higher refractive index than air,
so the light ray is slower in water than in air. The broken line perpendicular to the air-water interface is called the normal to the surface.
The light passing through air and striking the air-water boundary is called the incident ray,
while the ray after passing through the second medium is called the refracted ray.
The angle the incident ray makes with the normal to the surface is called the angle of incidence.
When light passes from a material with a lower refractive index to one with a higher value,
its speed decreases, and the refracted ray changes direction toward the normal. The angle between the refracted ray and the normal to the surface is called the angle of refraction.
.
If a light ray passes from water into air instead, its direction also changes. Its speed increases as it moves from a material with a higher refractive index to a lower one. In this case, it bends away from the normal.
Source
https://ophysics.com/em4.html
🧮 Calculator
🗑️
✏️ قلم
Vibrations and Waves |


Periodic Motion
Vibrational motion is a periodic motion where an object oscillates around an equilibrium position
We will study a special case of vibrational motion called Simple Harmonic Motion
Simple Harmonic Motion: A type of vibrational motion in a straight line around an equilibrium position where the restoring force is directly proportional to the displacement of the object and opposite in direction Some characteristics of Simple Harmonic Motion
Amplitude
The maximum displacement of the object from the equilibrium position
\[A\]
Frequency
The number of complete oscillations per second
\[f\]
Period is the time required to complete one full cycle
\[T\]
Hooke's Law: Force = Spring Constant × Displacement (F = kx) Simple Pendulum: A weight at the end of a weightless, inextensible string
with the other end fixed
Restoring Force \[F= - mg .sin (𝜃)\]
Because the string tension is perpendicular to the direction of motion, and the restoring force is negative because the force component is always opposite to the displacement
We consider the pendulum motion as simple harmonic motion if the pendulum is displaced by an angle less than 15 degrees
In this simulation we will study the factors affecting the period of a pendulum moving in simple harmonic motion

Hooke's Law
Hooke's Law is the law of elasticity discovered by English scientist Robert Hooke in 1660,
which states that for relatively small deformations of an object,
the displacement or size of the deformation is directly proportional to the deforming force or compression,
and under these conditions the object returns to its original shape and size when the force is removed,
The elastic behavior of solids can be explained by Hooke's Law: the deformation of molecules composed of atoms or ions
is directly proportional to the force causing this displacement, and opposite in direction. Mathematically, Hooke's Law is expressed as:
F = - kx
Hooke's Law Simulation Experiment
Mass (grams)
Force (Newton)
Extension (cm)
Hooke's Constant (N/m)
-
-
-
and determine the restoring force, displacement, kinetic energy and potential energy of an object oscillating around the equilibrium position
Physics Short Quiz
Simple Harmonic Motion
The Pendulum
Pendulum Period Simulation Experiment
Trial Number
Angle (degrees)
Pendulum Length (m)
Time for 10 oscillations (s)
Time for one oscillation (s)
1
10
2
10
3
10
4
10
5
10
Pendulum Length vs Period Relationship
Period Squared vs Length Relationship
Mechanical Waves
Medium - The matter through which the wave travels
Mechanical Waves: Waves that require a physical medium to travel through. Example - Sound waves. Sound waves cannot travel through a vacuum.
When a mechanical wave moves through a physical medium, the particles in the medium oscillate with simple harmonic motion.
Simple Harmonic Motion
The blue ball above is in simple harmonic motion. Imagine this ball represents a particle in a solid material. If this particle is connected to other nearby particles, its motion would affect the motion of surrounding particles.

Transverse Wave
In the diagram above, the motion of the leftmost particle causes the adjacent particle to oscillate.
This oscillation is passed down through the entire chain of particles. Notice that the particles vibrate up and down (vertically)
, while the wave itself moves from left to right (horizontally). This specific type of wave motion is called a transverse wave
.
Transverse Wave - A wave in which the particles of the medium move perpendicular to the direction of wave motion.
Waves can also move through matter when the particles of the medium vibrate back and forth in the direction of wave motion. This type of wave is called a longitudinal wave.
Longitudinal Waves - A wave in which the particles of the medium move parallel to the direction of wave motion.
Longitudinal Waves
In the longitudinal wave above, the leftmost particle vibrates horizontally with simple harmonic motion
, causing the particles to its right to also vibrate with simple harmonic motion
. The wave energy is transferred horizontally to the right.
Transverse mechanical waves can only move through solids, while longitudinal waves can move through solids, liquids and gases.
Surface Waves
Surface Waves:Longitudinal waves originate in the depths of oceans.
While water particles on the surface follow a circular path.
. Sometimes parallel to the wave motion and sometimes perpendicular to the wave motion
Wave Properties and Terminology
Waves have properties closely related to the properties of particle vibrations. The wave period, frequency, and amplitude are defined in the same way as particle oscillations and their frequency and amplitude:
Period - The time required to complete one full vibration. (SI unit: second)
Frequency - The number of vibrations per second. (SI unit: Hertz or inverse second)
Amplitude - The maximum displacement from the equilibrium position. (SI unit: meter)
Wavelength - The distance from one crest to another (or between any two consecutive points in phase). (SI unit: meter)
To explore some properties of transverse and longitudinal waves. Adjust the amplitude and frequency sliders and observe how the waves are affected. Click the "Play" button to start the wave motion. Note that the entire transverse wave has a single equilibrium line, while in longitudinal waves, each particle in the medium has its own equilibrium position.
The speed of a wave depends on the medium through which it travels, not on its frequency or wavelength.
The frequency of a wave is determined by the source that produces the wave - it does not depend on the medium through which the wave travels.
The wavelength of a wave depends on both the speed and frequency of the wave:
\[λ=\frac{v}{f}\]
Wave Behavior
When a wave reaches a boundary, which is a point where the medium changes, i.e., when it moves to another medium, three things happen. Part of the wave is transmitted to the new medium, some of the wave is reflected back into the original medium, and some of the wave's energy is absorbed. When the new medium is denser, the wave inverts upon reflection (fixed barrier), and when it is less dense, it reflects in the same direction (free barrier)


The animation above shows the entire wave pulse being reflected back into the original medium. In reality, some of the wave pulse's energy would be transmitted to the new medium, and the reflected pulse would have a smaller amplitude (less energy) than the original pulse. Also note that the speed of the reflected wave pulse is the same as the speed of the incident wave pulse. The speed depends on the medium, and the reflected pulse is still in the original medium, so it has the same speed as the incident pulse.
Use the simulation below to explore and think in more detail. It allows you to see how the incoming and reflected pulses combine to form the actual visible pulse on the string.
When two or more waves interfere in the same medium at the same time, it is referred to as wave interference. The process of interference is easier to understand by observing interfering wave pulses. Use the simulation below to explore the interference of wave pulses. Experiment with waves of different widths and heights, including negative height pulses interfering with positive height pulses.
Note that the wave pulses do not bounce off each other; instead, they pass directly through each other and continue on their way as if nothing happened. This is known as the (principle of independence), and the effect is only visible when they interfere. When two pulses interfere, the resulting wave is the algebraic sum of the two pulses. This is known as the (superposition principle). The superposition principle can be defined as follows: the displacement of the medium from its equilibrium position when multiple waves interfere is equal to the algebraic sum of the displacements of the individual waves.

Interference of Multiple Pulses
When multiple pulses interfere, the superposition principle and the principle of independence are applied. The colored dotted lines in the animation show the original shape of the pulses, while the black line shows the actual appearance we see, which is the sum of the original pulses.
Many different interference patterns can appear when two waves interfere. Here are some examples.
In the simulation above, the blue and red waves are moving in the same direction in the same medium (and thus have the same speed). The purple wave at the bottom shows the sum of the blue and red waves. Use the checkbox to see the red and blue waves superimposed on each other. Use the play button in the lower left corner to start the animation. By default, the red and blue waves have the same wavelength and are "in phase". When transverse waves are in phase, they match crest to crest. The sum of the two waves has twice the amplitude of either of the original waves. This is called constructive interference. Use the slider to change the phase of the blue wave. Watch how their sum becomes smaller as the phase difference increases. It is possible for destructive interference to occur, where the waves completely cancel each other out.
Now set the two wavelengths to very different values, for example, try 1.5 for one and 2.5 for the other. Their sum now appears alongside each of the individual waves. This can lead to very complex wave combinations.
When two waves move in the same medium but in opposite directions, different interference patterns form. If two waves moving in opposite directions have the same wavelength, the interference pattern is known as a standing wave
In the simulation shown above, the red and blue waves are moving in the same medium but in opposite directions. When the two waves have different wavelengths, their sum is a complex traveling wave. Now set both wavelengths to the same value (this can also be done by clicking the Show Standing Wave button). Their sum is a special type of wave interference known as a standing wave. A standing wave is called so because it does not move in the direction of either wave. Some points on the standing wave do not move at all; these points are called nodes. The points on the standing wave that undergo the maximum displacement are called antinodes. Use the checkbox to observe the nodes and antinodes.

Fundamental Frequency (First Standing Wave)
\[f = f_0 \]\[L =\frac{λ}{2}\]\[λ = 2L\]
There are many other vibration modes for a string fixed at both ends. Each mode is called a harmonic. In the second harmonic, the standing wave consists of two parts. The wavelength is half the fundamental wavelength, and thus the frequency is twice the fundamental frequency.
Second Harmonic Wave
\[f = 2f_0\] \[L = λ\] \[λ = L\]
In the third harmonic, the standing wave consists of three parts. The wavelength is one-third of the fundamental wavelength, and thus the frequency is three times the fundamental frequency.

Third Harmonic Wave
\[f = 3f_0\] \[L = \frac{3λ}{2}\] \[λ = \frac{2L}{3}\]

The white lines are called wavefronts, and the black lines represent the trough. Each ring is a set of points reached by the vibration at the same time period.
We call the distance between one wavefront and the next the wavelength.
Or the distance between two consecutive troughs is the wavelength.
The wave propagates in all directions, and the direction of wave propagation is always perpendicular to the wavefront.
When a wave hits an obstacle or reaches the end of the medium it is traveling through,
part of the wave is reflected back into the original medium. It is reflected back at an angle equal to the angle of incidence. These angles are called the angle of incidence and the angle of reflection.
The normal line, incident and reflected rays, and the angles of incidence and reflection are shown in this simulation. The law of reflection states that the angle of incidence is equal to the angle of reflection.
The rules of reflection apply, and this is what happens when water waves bounce off the side of a pond.
Wave refraction: is the bending of waves as they pass from one medium to another. When a wave hits the surface of a different medium, some of it is reflected, while some bends and changes direction as it passes through the medium.
A light ray passes from air into water. Note that water has a higher refractive index than air,
so the light ray is slower in water than in air. The broken line perpendicular to the air-water interface is called the normal to the surface.
The light passing through air and striking the air-water boundary is called the incident ray,
while the ray after passing through the second medium is called the refracted ray.
The angle the incident ray makes with the normal to the surface is called the angle of incidence.
When light passes from a material with a lower refractive index to one with a higher value,
its speed decreases, and the refracted ray changes direction toward the normal. The angle between the refracted ray and the normal to the surface is called the angle of refraction.
.
If a light ray passes from water into air instead, its direction also changes. Its speed increases as it moves from a material with a higher refractive index to a lower one. In this case, it bends away from the normal.
Source
https://ophysics.com/em4.html
 Physics
Physics
No comments:
Post a Comment