00971504825082
Current and Resistance

Electric Current
Electric Current
:It is the flow of electric charges in an electrical conductor. The electric charge can be either electrons or ions
According to the International System of Units, electric current is measured in amperes
While electric current is measured with a device called an ammeter
In this simulation, close the circuit and observe the movement of electric charges and how they lose energy in the resistor
In this simulation, the movement of electrons in a simple circuit from the lowest to the highest voltage is represented. Note that the term "electric current" means the movement of positive charges from the higher to the lower voltage

Current Density
It is the current flowing per unit area in a conducting wire at a specific point. Current density is denoted by the symbol
j
It is a vector quantity whose direction is the same as the movement of positive charges (opposite to the movement of electrons)
\[j=\frac{i}{A}\] and is measured in units of \[\frac{A}{m^2}\]
Drift velocity is the directed velocity of electrons in an electrical circuit.
Any conducting wire contains electrons moving randomly at high speed. When a potential difference is applied across the wire, the electrons' movement becomes a directed random velocity called drift velocity, which is very slow, on the order of
\[𝜗_d =10^{-4}\frac {m}{s}\]

We have a conductor with cross-sectional area (A)
(𝜗𝑑) and an electric field is applied to it. The electrons move opposite to the field with a drift velocity
(d t) and during a time interval of
it travels a distance of
\[𝜗𝑑 . dt\] and thus the volume of electrons passing through the cross-section equals
\[A. 𝜗𝑑 . dt\] so the number of electrons in this volume equals
\[n . A. 𝜗𝑑 . dt\]
(-e) and each electron is charged with a charge of
Therefore, the charge flowing through this area
\[dq = - e. n . A. 𝜗𝑑 . dt\]
Then we get the current intensity
\[i =\frac{ dq }{ dt }= - e. n . A. 𝜗𝑑\]
And current density
\[j = \frac{i}{A} = - e. n . 𝜗𝑑\]

\[1 \star \]

Ohm's Law
In this simulation, Ohm studied the relationship between current intensity and voltage across an ohmic resistor. Choose a value for an ohmic resistance and change the voltage each time. Observe what happens to the current intensity. Repeat the experiment with another resistance
Ohm's Law Experiment
Ohm's Law Experiment - Complete the following table
Experiment No.
Voltage (Volt)
Current (Ampere)
Resistance (Ohm)
1
2
3
4
5
Ohm's Law
Ohm's Law is a fundamental principle in electricity, named after the German physicist "Georg Simon Ohm".
It states that the potential difference across a metallic conductor is directly proportional to the current flowing through it.
The constant ratio between voltage and current is defined as electrical resistance. It is noted that the resistance of a conductor is a constant value and does not change with the change in potential difference across its ends.
The equation can be expressed as follows:
\[ V = I . R \]
Test yourself

Resistivity and Resistance
Electrical resistance: It is the extent to which a material opposes the flow of electric current
When a potential difference is applied across a wire
\[∆V \] and a current of intensity \[i\] passes through it,
the wire's opposition to the current is given by the relation according to Ohm's law \[R=\frac {∆V}{i}\]
The unit of electrical resistance is ohm, which equals \[𝝮=\frac{V}{A}\]
Some devices are described in terms of their ability to conduct rather than their ability to oppose current
\[G\] which is measured in Siemens \[G=\frac {i}{∆V}=\frac {1}{R}\;\;\;\;\;\;\;\;\;\;\;\;\;\;S=\frac {A}{V}=\frac {1}{𝝮}\]
The resistance of any wire to current flow depends on the material it is made of, its geometric shape, and temperature.
Each wire has a specific resistance called resistivity \[𝜌\], which is the ratio between the electric field intensity and current density
\[𝜌=\frac {E}{J}\;\;\;\;\;\;\;\;\;\;\;𝜌=\frac {\frac {V}{m}}{\frac {A}{m^2}}=\frac {V.m}{A}=𝝮.m\]
Resistivity and Temperature Coefficient of Resistivity for Some Conductors
\[∝\] Temperature coefficient at temperature
\[20^0c\]\[×10^{-3}\;\;K^{-1}\]
\[ 𝜌\] Resistivity at temperature
\[20^0c\]\[×10^{-8}\;\;𝝮.m\]
Material Name
3.8
1.6
Silver
3.9
1.72
Copper
3.4
2.44
Gold
3.9
2.82
Aluminum
2
3.9
Brass
4.5
5.51
Tungsten
5
9.7
Iron
We know that
\[E=\frac{∆V}{L}\;\;\;\;\;\;\;\;\;J=\frac{i}{A}\]
\[𝜌=\frac {E}{J}=\frac {\frac{∆V}{L}}{\frac{i}{A}}=\frac{∆V.A}{i.L}=\frac{iR.A}{i.L}=\frac{R.A}{L}\]
\[R= 𝜌.\frac{A}{L}\]
Factors Affecting Ohmic Resistance
In this simulation, we observe that the resistance value changes with changes in resistor length, cross-sectional area, and the material the resistor is made of
\[2 \star \]
Current and Resistance |

Electric Current
Electric Current
:It is the flow of electric charges in an electrical conductor. The electric charge can be either electrons or ions
According to the International System of Units, electric current is measured in amperes
While electric current is measured with a device called an ammeter
In this simulation, close the circuit and observe the movement of electric charges and how they lose energy in the resistor
In this simulation, the movement of electrons in a simple circuit from the lowest to the highest voltage is represented. Note that the term "electric current" means the movement of positive charges from the higher to the lower voltage
Current Density
It is the current flowing per unit area in a conducting wire at a specific point. Current density is denoted by the symbol
j
It is a vector quantity whose direction is the same as the movement of positive charges (opposite to the movement of electrons)
\[j=\frac{i}{A}\] and is measured in units of \[\frac{A}{m^2}\]
Drift velocity is the directed velocity of electrons in an electrical circuit. Any conducting wire contains electrons moving randomly at high speed. When a potential difference is applied across the wire, the electrons' movement becomes a directed random velocity called drift velocity, which is very slow, on the order of \[𝜗_d =10^{-4}\frac {m}{s}\]
We have a conductor with cross-sectional area (A)
(𝜗𝑑) and an electric field is applied to it. The electrons move opposite to the field with a drift velocity
(d t) and during a time interval of
it travels a distance of \[𝜗𝑑 . dt\] and thus the volume of electrons passing through the cross-section equals \[A. 𝜗𝑑 . dt\] so the number of electrons in this volume equals \[n . A. 𝜗𝑑 . dt\]
(-e) and each electron is charged with a charge of
Therefore, the charge flowing through this area
\[dq = - e. n . A. 𝜗𝑑 . dt\] Then we get the current intensity \[i =\frac{ dq }{ dt }= - e. n . A. 𝜗𝑑\]
And current density \[j = \frac{i}{A} = - e. n . 𝜗𝑑\]
\[1 \star \]
Ohm's Law
In this simulation, Ohm studied the relationship between current intensity and voltage across an ohmic resistor. Choose a value for an ohmic resistance and change the voltage each time. Observe what happens to the current intensity. Repeat the experiment with another resistance
Ohm's Law Experiment - Complete the following table
| Experiment No. | Voltage (Volt) | Current (Ampere) | Resistance (Ohm) |
|---|---|---|---|
| 1 | |||
| 2 | |||
| 3 | |||
| 4 | |||
| 5 |
Ohm's Law
Ohm's Law is a fundamental principle in electricity, named after the German physicist "Georg Simon Ohm". It states that the potential difference across a metallic conductor is directly proportional to the current flowing through it. The constant ratio between voltage and current is defined as electrical resistance. It is noted that the resistance of a conductor is a constant value and does not change with the change in potential difference across its ends. The equation can be expressed as follows:
\[ V = I . R \]
Test yourself
Resistivity and Resistance
Electrical resistance: It is the extent to which a material opposes the flow of electric current
When a potential difference is applied across a wire \[∆V \] and a current of intensity \[i\] passes through it, the wire's opposition to the current is given by the relation according to Ohm's law \[R=\frac {∆V}{i}\] The unit of electrical resistance is ohm, which equals \[𝝮=\frac{V}{A}\] Some devices are described in terms of their ability to conduct rather than their ability to oppose current \[G\] which is measured in Siemens \[G=\frac {i}{∆V}=\frac {1}{R}\;\;\;\;\;\;\;\;\;\;\;\;\;\;S=\frac {A}{V}=\frac {1}{𝝮}\] The resistance of any wire to current flow depends on the material it is made of, its geometric shape, and temperature. Each wire has a specific resistance called resistivity \[𝜌\], which is the ratio between the electric field intensity and current density \[𝜌=\frac {E}{J}\;\;\;\;\;\;\;\;\;\;\;𝜌=\frac {\frac {V}{m}}{\frac {A}{m^2}}=\frac {V.m}{A}=𝝮.m\]
Resistivity and Temperature Coefficient of Resistivity for Some Conductors
|
\[∝\] Temperature coefficient at temperature \[20^0c\]\[×10^{-3}\;\;K^{-1}\] |
\[ 𝜌\] Resistivity at temperature \[20^0c\]\[×10^{-8}\;\;𝝮.m\] |
Material Name |
|
3.8 |
1.6 |
Silver |
|
3.9 |
1.72 |
Copper |
|
3.4 |
2.44 |
Gold |
|
3.9 |
2.82 |
Aluminum |
|
2 |
3.9 |
Brass |
|
4.5 |
5.51 |
Tungsten |
|
5 |
9.7 |
Iron |
We know that \[E=\frac{∆V}{L}\;\;\;\;\;\;\;\;\;J=\frac{i}{A}\] \[𝜌=\frac {E}{J}=\frac {\frac{∆V}{L}}{\frac{i}{A}}=\frac{∆V.A}{i.L}=\frac{iR.A}{i.L}=\frac{R.A}{L}\] \[R= 𝜌.\frac{A}{L}\]
Factors Affecting Ohmic Resistance
In this simulation, we observe that the resistance value changes with changes in resistor length, cross-sectional area, and the material the resistor is made of
\[2 \star \]
 Physics
Physics
 Click here to show solution
Click here to show solution





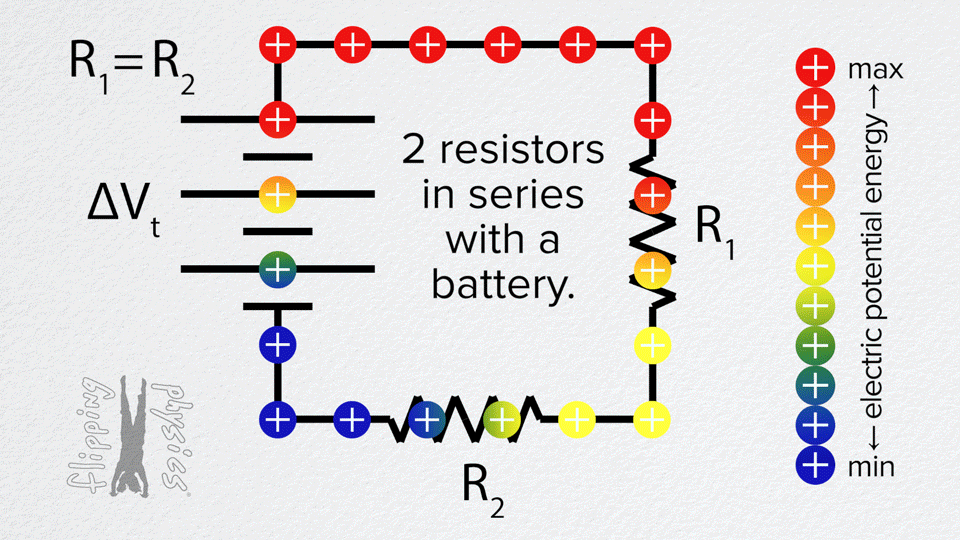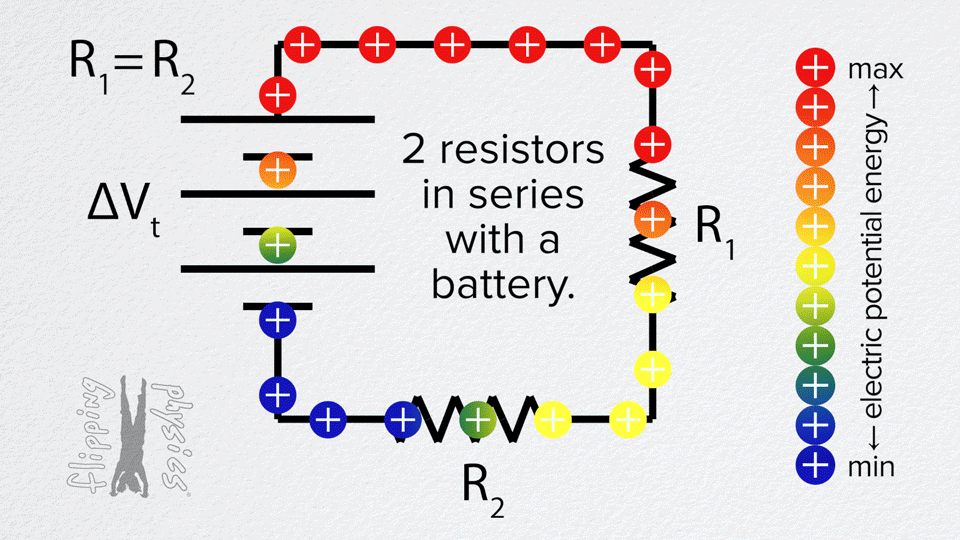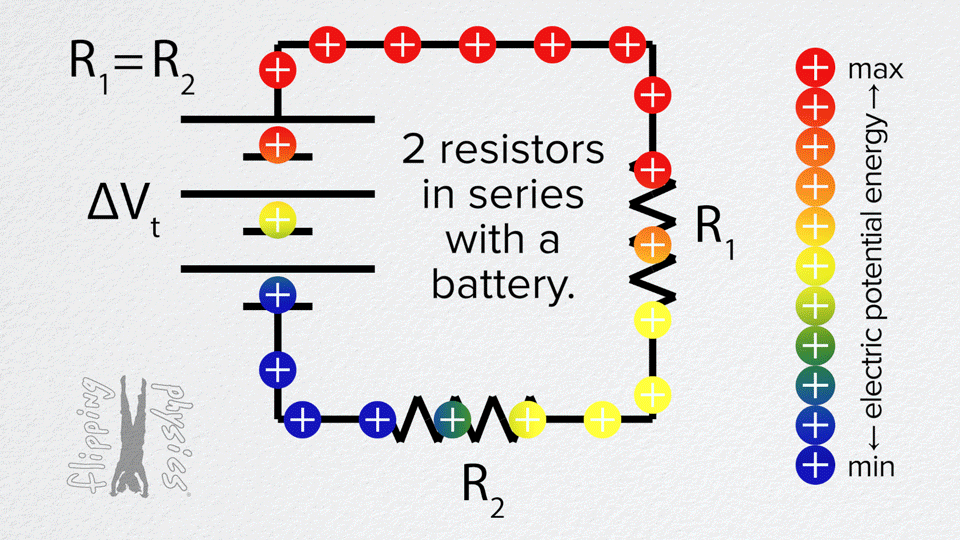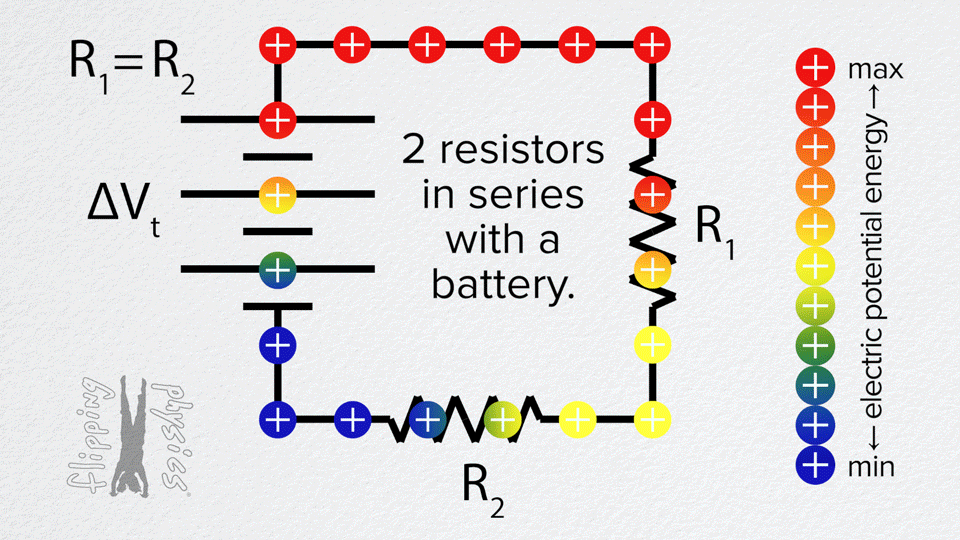
 If the internal resistance is neglected, then the electromotive force equals
If the internal resistance is neglected, then the electromotive force equals

















No comments:
Post a Comment