📄 Print pdf
00971504825082
Magnetic Field Produced by Direct Current
Magnetic Field Around a Current-Carrying Wire
Magnetic Field Around a Current-Carrying Wire
Basic Law
\[ B = \frac {(μ₀ * I) }{(2πr)}\]
Affecting Factors:
- Current Intensity (I): Field strength increases proportionally with current
- Distance from Wire (r): Field strength decreases inversely with distance
- Medium Permeability (μ₀): Property of the surrounding medium (in vacuum μ₀ = 4π×10⁻⁷ T·m/A)
Physical Explanation:
When electric current passes through a wire, a circular magnetic field is created around the wire according to the right-hand rule:
Practical Applications:
- Electric motors
- Electric generators
- Circuit breakers
- Electrical measuring devices
- Wired communication systems
Interactive Calculation
Enter values to calculate magnetic field strength:
When current passes through a conducting wire, a magnetic field is generated around the wire. Evidence for this is the arrangement of iron filings around the wire forming concentric circles that become less dense as you move away from the wire, indicating a non-uniform field. The field direction can be determined using the right-hand grip rule - with the thumb pointing in the current direction, the fingers curl in the field direction. The field strength changes with distance from the wire, current intensity, and the insulating medium.
Magnetic Field Around a Circular Wire
Magnetic Field Around a Circular Wire
Scientific Theory:
When electric current passes through a circular wire (loop):
- A magnetic field perpendicular to the loop plane is generated
- Field direction follows the right-hand rule
- Magnetic field strength (B) depends on:
- Current intensity (I)
- Loop radius (r)
- Number of turns (n)
Mathematical Law:
Field strength at loop center:
\[ B = \frac {(μ₀ * n * I) }{ (2r)}\]
Where:
μ₀ = Vacuum permeability (4π × 10⁻⁷ T·m/A)
n = Number of turns
I = Current intensity (Ampere)
r = Radius (meter)
Practical Applications:
- Electromagnets:
Multiple loops (coils) are used to create strong magnetic fields
- Electric Motors:
Generating rotating magnetic fields using alternating currents
- Magnetic Resonance Imaging (MRI):
Superconducting coils generate high-precision magnetic fields
- Electrical Transformers:
Power transfer through electromagnetic induction between coils
- Speakers:
Converting electrical signals to mechanical vibrations
Passing a current through a circular coil generates a magnetic field at each end with concentric circles, and a uniform field at the center of the coil.
Magnetic Field of a Current-Carrying Coil
Magnetic Field of a Current-Carrying Coil
Scientific Explanation:
When an electric current passes through a coil, a magnetic field is generated around the coil according to Ampère's law. The strength of this field is proportional to:
- Electric current intensity (I)
- Number of turns (N)
- Core material of the coil (μ)
Mathematical Formula:
\[B =\frac { μ₀ × μ_r × (N × I) }{ L}\]
Where:
B: Magnetic field intensity (Tesla)
μ₀: Permeability of free space (4π × 10-7)
μr: Relative permeability of the material
N: Number of turns
I: Current intensity (Ampere)
L: Length of the coil (meter)
Practical Applications:
1. Electrical Transformers
Use two opposing coils to transfer electrical energy while changing voltage through electromagnetic induction
2. Electric Motors
Generate rotating magnetic fields to convert electrical energy into kinetic energy
3. Magnetic Resonance Imaging (MRI)
Create very strong magnetic fields to image internal body tissues
4. Electrical Relays
Use magnetic fields to automatically open or close electrical circuits
Information Summary:
✓ Field strength increases with current or number of turns
✓ Ferromagnetic materials increase field strength by μr
✓ Applications depend on controlling field intensity and direction
✓ Efficiency depends on coil design and core material type
Passing current through a solenoid generates a magnetic field
with a non-uniform field outside the coil and a uniform field at its center
Evidence for this is seen in how iron filings arrange themselves inside and around the coil
forming closed curves inside the coil
Along the coil's axis, a uniform field forms whose direction can be determined using the right-hand grip rule
where fingers point in the current direction and the thumb shows the field direction (thumb points to north pole)
The field value along the coil's axis changes with the number of turns, current intensity, coil length, and insulating medium type
Passing current through a solenoid generates a magnetic field with a non-uniform field outside and a uniform field at its center
Magnetic Field Produced by Direct Current |
Magnetic Field Around a Current-Carrying Wire
Basic Law
Affecting Factors:
- Current Intensity (I): Field strength increases proportionally with current
- Distance from Wire (r): Field strength decreases inversely with distance
- Medium Permeability (μ₀): Property of the surrounding medium (in vacuum μ₀ = 4π×10⁻⁷ T·m/A)
Physical Explanation:
When electric current passes through a wire, a circular magnetic field is created around the wire according to the right-hand rule:
Practical Applications:
- Electric motors
- Electric generators
- Circuit breakers
- Electrical measuring devices
- Wired communication systems
Interactive Calculation
Enter values to calculate magnetic field strength:
When current passes through a conducting wire, a magnetic field is generated around the wire. Evidence for this is the arrangement of iron filings around the wire forming concentric circles that become less dense as you move away from the wire, indicating a non-uniform field. The field direction can be determined using the right-hand grip rule - with the thumb pointing in the current direction, the fingers curl in the field direction. The field strength changes with distance from the wire, current intensity, and the insulating medium.
Magnetic Field Around a Circular Wire
Scientific Theory:
When electric current passes through a circular wire (loop):
- A magnetic field perpendicular to the loop plane is generated
- Field direction follows the right-hand rule
- Magnetic field strength (B) depends on:
- Current intensity (I)
- Loop radius (r)
- Number of turns (n)
Mathematical Law:
Field strength at loop center:
\[ B = \frac {(μ₀ * n * I) }{ (2r)}\]
Where:
μ₀ = Vacuum permeability (4π × 10⁻⁷ T·m/A)
n = Number of turns
I = Current intensity (Ampere)
r = Radius (meter)
Practical Applications:
- Electromagnets:
Multiple loops (coils) are used to create strong magnetic fields
- Electric Motors:
Generating rotating magnetic fields using alternating currents
- Magnetic Resonance Imaging (MRI):
Superconducting coils generate high-precision magnetic fields
- Electrical Transformers:
Power transfer through electromagnetic induction between coils
- Speakers:
Converting electrical signals to mechanical vibrations
Magnetic Field of a Current-Carrying Coil
Scientific Explanation:
When an electric current passes through a coil, a magnetic field is generated around the coil according to Ampère's law. The strength of this field is proportional to:
- Electric current intensity (I)
- Number of turns (N)
- Core material of the coil (μ)
Mathematical Formula:
Where:
B: Magnetic field intensity (Tesla)
μ₀: Permeability of free space (4π × 10-7)
μr: Relative permeability of the material
N: Number of turns
I: Current intensity (Ampere)
L: Length of the coil (meter)
Practical Applications:
1. Electrical Transformers
Use two opposing coils to transfer electrical energy while changing voltage through electromagnetic induction
2. Electric Motors
Generate rotating magnetic fields to convert electrical energy into kinetic energy
3. Magnetic Resonance Imaging (MRI)
Create very strong magnetic fields to image internal body tissues
4. Electrical Relays
Use magnetic fields to automatically open or close electrical circuits
Information Summary:
✓ Field strength increases with current or number of turns
✓ Ferromagnetic materials increase field strength by μr
✓ Applications depend on controlling field intensity and direction
✓ Efficiency depends on coil design and core material type
Passing current through a solenoid generates a magnetic field
with a non-uniform field outside the coil and a uniform field at its center Evidence for this is seen in how iron filings arrange themselves inside and around the coil
forming closed curves inside the coil
Along the coil's axis, a uniform field forms whose direction can be determined using the right-hand grip rule
where fingers point in the current direction and the thumb shows the field direction (thumb points to north pole)
The field value along the coil's axis changes with the number of turns, current intensity, coil length, and insulating medium type
Passing current through a solenoid generates a magnetic field with a non-uniform field outside and a uniform field at its center
 Physics
Physics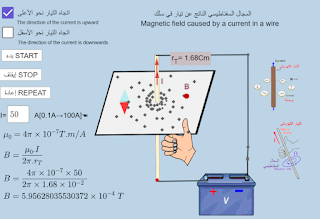
No comments:
Post a Comment