00971504825082
Kirchhoff's Questions Bank |
\[1\star\]
In the circuit below, the current intensity \[ I_2 =?\]
\[i_2 =7 \;A\;\;\;\;\;\; -C \]
\[i_2 =15 \;A\;\;\;\;\;\; -A \]
\[i_2 = 3 \;A\ \;\;\;\;\;\; -D \]
\[i_2 =5 \;A \;\;\;\;\;\; -B \]
Click here to show solution
Choose the correct answer
\[2\star\]
In the loop marked with number 1
The potential difference across the resistor \[ V_{R2} = ? \]
\[ 𝑉_{𝑅2 }= 15.25 \;𝑉 \;\;\;\;\;\; -C \]
\[𝑉_{𝑅2 }= 8.75 \;𝑉 \;\;\;\;\;\; -A \]
\[𝑉_{𝑅2 }= 5.36 \;𝑉 \;\;\;\;\;\; -D \]
\[𝑉_{𝑅2 }= 15.25 \;𝑉 \;\;\;\;\;\; -B \]
Click here to show solution
Choose the correct answer
\[3\star\]
In the figure below, the current passing through \[ R_1 , R_2 \] is equivalent to
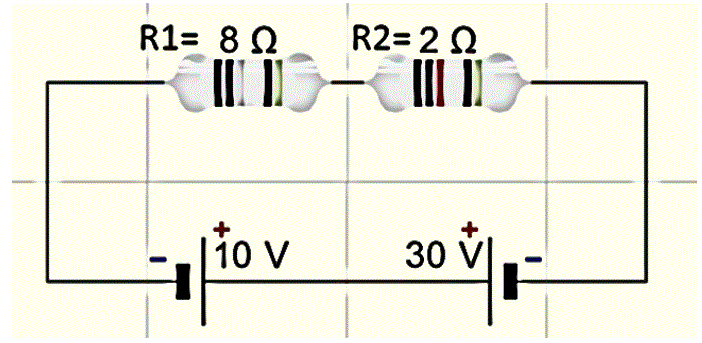
\[I_1 = 2\;A \;\;\;\;\;\;, \;\;\;\;\;\;I_2 =2 \;A -C \]
\[I_1 = 1\;A \;\;\;\;\;\;, \;\;\;\;\;\;I_2 =4 \;A -A \]
\[I_1 = 1\;A \;\;\;\;\;\;, \;\;\;\;\;\;I_2 =4 \;A -D \]
\[I_1 = 1\;A \;\;\;\;\;\;, \;\;\;\;\;\;I_2 =1 \;A -B \]
Click here to show solution
Choose the correct answer
\[4\star\]
In the figure below, using Kirchhoff's laws, calculate the value of the unknown resistance \[ R= .... \]
\[ R = 4\; Ω \;\;\;\;\;\; -C \]
\[R = 2\; Ω \;\;\;\;\;\; -A \]
\[R = 5\; Ω \;\;\;\;\;\; -D \]
\[R =3\; Ω\;\;\;\;\;\; -B \]
Click here to show solution
Choose the correct answer
\[5\star\]
In the figure below, using Kirchhoff's laws, the value of the unknown resistance \[ R= .... \]
equals
\[ R = 15\; Ω \;\;\;\;\;\; -C \]
\[R = 5\; Ω \;\;\;\;\;\; -A \]
\[R = 20\; Ω \;\;\;\;\;\; -D \]
\[R =10\; Ω\;\;\;\;\;\; -B \]
Click here to show solution
Choose the correct answer
\[6\star\]
In the figure below, using Kirchhoff's laws, the value of the unknown resistance \[ R= .... \] is equivalent to
\[ R = 10\; Ω \;\;\;\;\;\; -C \]
\[R = 8\; Ω \;\;\;\;\;\; -A \]
\[R = 6\; Ω \;\;\;\;\;\; -D \]
\[R =9\; Ω\;\;\;\;\;\; -B \]
Click here to show solution
Choose the correct answer
\[7\star \star\]
In the adjacent figure, the value of the variable resistance was changed until the galvanometer reading became zero. The value of the resistance \[ R_ X = .... \]
\[ R = 5\; Ω \;\;\;\;\;\; -C \]
\[R = 4\; Ω \;\;\;\;\;\; -A \]
\[R = 3\; Ω \;\;\;\;\;\; -D \]
\[R =6\; Ω\;\;\;\;\;\; -B \]
Click here to show solution
Choose the correct answer
\[8\star \]
The potential difference across the galvanometer equals zero
when the resistance values equal
Click here to show solution
Choose the correct answer
\[9\star \star\]
An ammeter is used to measure current and is connected in series in the circuit. To increase the range of the ammeter for measurement, connect
High resistance in parallel -C
Small resistance in parallel -A
High resistance in series -D
Small resistance in series -B
Click here to show solution
Choose the correct answer
\[10 \star\]
A voltmeter is used to measure potential difference and is connected in parallel in the circuit. To increase the range of the voltmeter for measurement, connect
High resistance in parallel -C
Small resistance in parallel -A
High resistance in series -D
Small resistance in series -B
Click here to show solution
Choose the correct answer
\[11 \star\]
An ammeter is used to measure low currents. Its internal resistance is 2Ω. A learner wanted to double its ability to measure current by 50 times. The value of the resistance that needs to be connected in parallel to achieve the desired result equals
\[ R = 0.04\; Ω \;\;\;\;\;\; -C \]
\[R = 0.02\; Ω \;\;\;\;\;\; -A \]
\[R = 0.05\; Ω \;\;\;\;\;\; -D \]
\[R =0.03\; Ω\;\;\;\;\;\; -B \]
Click here to show solution
Choose the correct answer
\[12 \star\]
A voltmeter is used to measure a potential difference of 1v. Its internal resistance is 500Ω. A learner wanted to make the device capable of measuring a potential difference of 50v. The value of the resistance that needs to be connected in series to achieve the desired result equals
\[ R = 37000 \; Ω \;\;\;\;\;\; -C \]
\[R = 40000\; Ω \;\;\;\;\;\; -A \]
\[R = 54000\; Ω \;\;\;\;\;\; -D \]
\[R =24500 \; Ω\;\;\;\;\;\; -B \]
Click here to show solution
Choose the correct answer
\[13 \star\]
In the figure below at junction A, one of the following statements is correct
\[𝐼_2+𝐼_3=𝐼_1 \;\;\;\;\;\; -C \]
\[𝐼_2+𝐼_5+𝐼_4=𝐼_1 \;\;\;\;\;\; -A \]
\[𝐼_3+𝐼_5+𝐼_4=𝐼_1 \;\;\;\;\;\; -D \]
\[𝐼_2+𝐼_3+𝐼_5=𝐼_1 \;\;\;\;\;\; -B \]
Click here to show solution
Choose the correct answer
\[14 \star\]
In the circuit below, the battery voltage equals
\[E=250 \;\;V\;\;\;\;\;\;-C\]
\[E=300 \;\;V\;\;\;\;\;\;-A\]
\[E=350 \;\;V\;\;\;\;\;\;-D\]
\[E=150 \;\;V\;\;\;\;\;\;-B\]
Click here to show solution
Choose the correct answer
\[15 \star\]
In the figure below, the potential difference across
the first and third resistors
respectively equals
\[V1=7\; V \;\;\;\;\;\; ,\;\;\;\;\;\; V3=5 \;V-C\]
\[V1=7\; V \;\;\;\;\;\; ,\;\;\;\;\;\; V3=2 \;V-A\]
\[V1=2\; V \;\;\;\;\;\; ,\;\;\;\;\;\; V3=7 \;V-D\]
\[V1=5\; V \;\;\;\;\;\; ,\;\;\;\;\;\; V3=7 \;V-B\]
Click here to show solution
Choose the correct answer
\[16\star \star\]
In the figure below, the value of resistance
\[R\] equals
\[ R = 3.33\; Ω \;\;\;\;\;\; -C \]
\[R = 6.42 \; Ω \;\;\;\;\;\; -A \]
\[R = 5.35\; Ω \;\;\;\;\;\; -D \]
\[R =2.5\; Ω\;\;\;\;\;\; -B \]
Click here to show solution
Choose the correct answer
\[17\star \star \star\]
In the figure below, the current passing through the
\[1Ω\] resistor equals
\[ 𝐼 =0.54 \;A \;\;\;\;\;\; -C \]
\[ 𝐼 =0.54 \;A \;\;\;\;\;\; -A \]
\[ 𝐼 =0.25 \;A \;\;\;\;\;\; -D \]
\[ 𝐼 =0.35 \;A\;\;\;\;\;\; -B \]
Click here to show solution
Choose the correct answer
\[18 \star\]
An ammeter with internal resistance
\[10 Ω\]
can measure current up to
\[8 mA\]. A student wanted to extend its range to measure current up to
\[2A\] by connecting a parallel resistor.
The required resistance value for this purpose is
\[ R_s = 0.08 \; Ω \;\;\;\;\;\; -C \]
\[R_s = 0.04 \; Ω \;\;\;\;\;\; -A \]
\[R_s = 0.01\; Ω \;\;\;\;\;\; -D \]
\[R_s =0.06\; Ω\;\;\;\;\;\; -B \]
Click here to show solution
Choose the correct answer
\[19 \star \star \star\]
A voltmeter has an internal resistance
\[1000 Ω\] and can measure a potential difference of
\[0.05 V\]. A student wanted to extend the device's range to measure a potential difference
\[ 10 V\], so a series resistor was connected to increase the device's range.
The required resistance value for this purpose equals
\[ R_{es}=199000 \; Ω \;\;\;\;\;\; -C \]
\[R_{es}=109000\; Ω \;\;\;\;\;\; -A \]
\[R_{es} = 250000\; Ω \;\;\;\;\;\; -D \]
\[R_{es} =165000\; Ω\;\;\;\;\;\; -B \]
Click here to show the solution
Choose the correct answer
\[20\star \star\]
A capacitor with capacitance
\[20𝜇𝐹\] uncharged was connected in series with a resistor
\[150 Ω\] and a battery as shown in the figure below. The percentage of capacitor charge after a time of
\[3 ms\] equals
\[ 0.47 \;\;\;\;\;\;-C\]
\[0. 75 \;\;\;\;\;\;-A\]
\[ 0.82 \;\;\;\;\;\;-D\]
\[0.63\;\;\;\;\;\;-B\]
Click here to show the solution
Choose the correct answer
\[21\star \star\]
A capacitor with capacitance
\[6𝜇𝐹 \] uncharged was connected in series with two resistors
\[ R_1=90 Ω ,R_2=30 Ω \] and a battery with voltage
\[50V\]. The time required to complete 50% charging of the capacitor equals
\[t =4.45 ×10^{-5 } \;\;S\;\;\;\;\;\;-C\]
\[t =9.35 ×10^{-5 } \;\;S\;\;\;\;\;\;-A\]
\[t =2.18 ×10^{-5 } \;\;S\;\;\;\;\;\;-D\]
\[t =6.86 ×10^{-5 } \;\;S\;\;\;\;\;\;-B\]
Click here to show the solution
Choose the correct answer
\[22 \star\]
A capacitor with capacitance
\[2𝜇𝐹\] was connected with two resistors
\[ R_1=500 Ω ,R_2=300 Ω \] and a battery until the charging process was completed as shown in the figure below. The time constant for completing the discharging process equals
\[𝜏=1.6×10^{-3} \;\;S\;\;\;\;\;\;-C\]
\[𝜏=2.6×10^{-3} \;\;S\;\;\;\;\;\;-A\]
\[𝜏=3.1×10^{-3} \;\;S\;\;\;\;\;\;-D\]
\[𝜏=4.2×10^{-3} \;\;S\;\;\;\;\;\;-B\]
Click here to show the solution
Choose the correct answer
\[23 \star\]
An electrical circuit consists of four resistors with values as shown in the figure below. The current intensity passing through each resistor is:
\[I_1=0.35 A \;\;\;, \;\;\;I_2=0.35 A \;\;\;, \;\;\;I_3=0.7 A \;\;\;\;\;\;-C\]
\[I_1=0.25 A \;\;\;, \;\;\;I_2=0.25 A \;\;\;, \;\;\;I_3=0.5 A \;\;\;\;\;\;-A\]
\[I_1=0.2 A \;\;\;, \;\;\;I_2=0.2 A \;\;\;, \;\;\;I_3=0.4 A \;\;\;\;\;\;-D\]
\[I_1=0.5 A \;\;\;, \;\;\;I_2=0.5 A \;\;\;, \;\;\;I_3=0.2 A \;\;\;\;\;\;-B\]
Click here to show solution Choose the correct answer
\[24 \star\]
In the figure below, an electrical circuit is shown with resistors, batteries, current direction, and positive direction indicated. One of the equations correctly represents the equation of one of the loops in the circuit (Kirchhoff's second law):
\[2−2I_1−2I_2−4I_3=0\;\;\;\;\;\;-C\]
\[6−I_1−2I_2=0 \;\;\;\;\;\;-A\]
\[4−I_1+4I_3=0\;\;\;\;\;\;-D\]
\[2−2I_1−2I_2−4I_3=0\;\;\;\;\;\;-B\]
Click here to show solution Choose the correct answer
\[25 \star\]
In the circuit below, the potential difference between points A and B equals:
\[∆𝑉=11.44\;\;V \;\;\;\;\;\;-C\]
\[∆𝑉=8.66\;\;V \;\;\;\;\;\;-A\]
\[∆𝑉=5.42\;\;V \;\;\;\;\;\;-D\]
\[∆𝑉=13.57\;\;V \;\;\;\;\;\;-B\]
Click here to show solution Choose the correct answer
\[26 \star\]
A Wheatstone bridge was constructed using a copper wire of length 2m with a sliding contact point. Two resistors were placed on the other end: \[R_1=80 Ω , R_2=R\]. The contact point was moved until the galvanometer reading became zero at contact point C, which is 0.4 m from the end of the wire A. The value of \[R_2\] equals:
\[ R_2 = 10\; Ω \;\;\;\;\;\; -C \]
\[R_2 = 20\; Ω \;\;\;\;\;\; -A \]
\[R _2= 30\; Ω \;\;\;\;\;\; -D \]
\[R_2 =40\; Ω\;\;\;\;\;\; -B \]
Click here to show solution Choose the correct answer
\[27\star \star\]
In the figure below, for loop 1 according to sign conventions and the assumed clockwise positive direction, one of the loop components has a negative voltage:
21 ohm resistor -C
5V battery -A
7V battery-D
10 ohm resistor-B
Click here to show solution Choose the correct answer
Solve the following problems
\[1 \star \]
In the circuit below, the current intensity \[ I_2 =?\]
\[i_2 =7 \;A\;\;\;\;\;\; -C \] |
\[i_2 =15 \;A\;\;\;\;\;\; -A \] |
\[i_2 = 3 \;A\ \;\;\;\;\;\; -D \] |
\[i_2 =5 \;A \;\;\;\;\;\; -B \] |
Click here to show solution
Choose the correct answer
In the loop marked with number 1
The potential difference across the resistor \[ V_{R2} = ? \]
\[ 𝑉_{𝑅2 }= 15.25 \;𝑉 \;\;\;\;\;\; -C \] |
\[𝑉_{𝑅2 }= 8.75 \;𝑉 \;\;\;\;\;\; -A \] |
\[𝑉_{𝑅2 }= 5.36 \;𝑉 \;\;\;\;\;\; -D \] |
\[𝑉_{𝑅2 }= 15.25 \;𝑉 \;\;\;\;\;\; -B \] |
Click here to show solution
Choose the correct answer
In the figure below, the current passing through \[ R_1 , R_2 \] is equivalent to
\[I_1 = 2\;A \;\;\;\;\;\;, \;\;\;\;\;\;I_2 =2 \;A -C \] |
\[I_1 = 1\;A \;\;\;\;\;\;, \;\;\;\;\;\;I_2 =4 \;A -A \] |
\[I_1 = 1\;A \;\;\;\;\;\;, \;\;\;\;\;\;I_2 =4 \;A -D \] |
\[I_1 = 1\;A \;\;\;\;\;\;, \;\;\;\;\;\;I_2 =1 \;A -B \] |
Click here to show solution
Choose the correct answer
\[ R = 4\; Ω \;\;\;\;\;\; -C \] |
\[R = 2\; Ω \;\;\;\;\;\; -A \] |
\[R = 5\; Ω \;\;\;\;\;\; -D \] |
\[R =3\; Ω\;\;\;\;\;\; -B \] |
Click here to show solution
Choose the correct answer
equals
\[ R = 15\; Ω \;\;\;\;\;\; -C \] |
\[R = 5\; Ω \;\;\;\;\;\; -A \] |
\[R = 20\; Ω \;\;\;\;\;\; -D \] |
\[R =10\; Ω\;\;\;\;\;\; -B \] |
Click here to show solution
Choose the correct answer
In the figure below, using Kirchhoff's laws, the value of the unknown resistance \[ R= .... \] is equivalent to
\[ R = 10\; Ω \;\;\;\;\;\; -C \] |
\[R = 8\; Ω \;\;\;\;\;\; -A \] |
\[R = 6\; Ω \;\;\;\;\;\; -D \] |
\[R =9\; Ω\;\;\;\;\;\; -B \] |
Click here to show solution
Choose the correct answer
In the adjacent figure, the value of the variable resistance was changed until the galvanometer reading became zero. The value of the resistance \[ R_ X = .... \]
\[ R = 5\; Ω \;\;\;\;\;\; -C \] |
\[R = 4\; Ω \;\;\;\;\;\; -A \] |
\[R = 3\; Ω \;\;\;\;\;\; -D \] |
\[R =6\; Ω\;\;\;\;\;\; -B \] |
Click here to show solution
Choose the correct answer
The potential difference across the galvanometer equals zero
when the resistance values equal
Click here to show solution
Choose the correct answer
An ammeter is used to measure current and is connected in series in the circuit. To increase the range of the ammeter for measurement, connect
High resistance in parallel -C |
Small resistance in parallel -A |
High resistance in series -D |
Small resistance in series -B |
Click here to show solution
Choose the correct answer
A voltmeter is used to measure potential difference and is connected in parallel in the circuit. To increase the range of the voltmeter for measurement, connect
High resistance in parallel -C |
Small resistance in parallel -A |
High resistance in series -D |
Small resistance in series -B |
Click here to show solution
Choose the correct answer
An ammeter is used to measure low currents. Its internal resistance is 2Ω. A learner wanted to double its ability to measure current by 50 times. The value of the resistance that needs to be connected in parallel to achieve the desired result equals
\[ R = 0.04\; Ω \;\;\;\;\;\; -C \] |
\[R = 0.02\; Ω \;\;\;\;\;\; -A \] |
\[R = 0.05\; Ω \;\;\;\;\;\; -D \] |
\[R =0.03\; Ω\;\;\;\;\;\; -B \] |
Click here to show solution
Choose the correct answer
A voltmeter is used to measure a potential difference of 1v. Its internal resistance is 500Ω. A learner wanted to make the device capable of measuring a potential difference of 50v. The value of the resistance that needs to be connected in series to achieve the desired result equals
\[ R = 37000 \; Ω \;\;\;\;\;\; -C \] |
\[R = 40000\; Ω \;\;\;\;\;\; -A \] |
\[R = 54000\; Ω \;\;\;\;\;\; -D \] |
\[R =24500 \; Ω\;\;\;\;\;\; -B \] |
Click here to show solution
Choose the correct answer
In the figure below at junction A, one of the following statements is correct
\[𝐼_2+𝐼_3=𝐼_1 \;\;\;\;\;\; -C \] |
\[𝐼_2+𝐼_5+𝐼_4=𝐼_1 \;\;\;\;\;\; -A \] |
\[𝐼_3+𝐼_5+𝐼_4=𝐼_1 \;\;\;\;\;\; -D \] |
\[𝐼_2+𝐼_3+𝐼_5=𝐼_1 \;\;\;\;\;\; -B \] |
Click here to show solution
Choose the correct answer
In the circuit below, the battery voltage equals
\[E=250 \;\;V\;\;\;\;\;\;-C\] |
\[E=300 \;\;V\;\;\;\;\;\;-A\] |
\[E=350 \;\;V\;\;\;\;\;\;-D\] |
\[E=150 \;\;V\;\;\;\;\;\;-B\] |
Click here to show solution
Choose the correct answer
In the figure below, the potential difference across the first and third resistors respectively equals
\[V1=7\; V \;\;\;\;\;\; ,\;\;\;\;\;\; V3=5 \;V-C\] |
\[V1=7\; V \;\;\;\;\;\; ,\;\;\;\;\;\; V3=2 \;V-A\] |
\[V1=2\; V \;\;\;\;\;\; ,\;\;\;\;\;\; V3=7 \;V-D\] |
\[V1=5\; V \;\;\;\;\;\; ,\;\;\;\;\;\; V3=7 \;V-B\] |
Click here to show solution
Choose the correct answer
In the figure below, the value of resistance \[R\] equals
\[ R = 3.33\; Ω \;\;\;\;\;\; -C \] |
\[R = 6.42 \; Ω \;\;\;\;\;\; -A \] |
\[R = 5.35\; Ω \;\;\;\;\;\; -D \] |
\[R =2.5\; Ω\;\;\;\;\;\; -B \] |
Click here to show solution
Choose the correct answer
In the figure below, the current passing through the \[1Ω\] resistor equals
\[ 𝐼 =0.54 \;A \;\;\;\;\;\; -C \] |
\[ 𝐼 =0.54 \;A \;\;\;\;\;\; -A \] |
\[ 𝐼 =0.25 \;A \;\;\;\;\;\; -D \] |
\[ 𝐼 =0.35 \;A\;\;\;\;\;\; -B \] |
Click here to show solution
Choose the correct answer
An ammeter with internal resistance
\[10 Ω\]
can measure current up to
\[8 mA\]. A student wanted to extend its range to measure current up to
\[2A\] by connecting a parallel resistor.
The required resistance value for this purpose is
\[ R_s = 0.08 \; Ω \;\;\;\;\;\; -C \] |
\[R_s = 0.04 \; Ω \;\;\;\;\;\; -A \] |
\[R_s = 0.01\; Ω \;\;\;\;\;\; -D \] |
\[R_s =0.06\; Ω\;\;\;\;\;\; -B \] |
Click here to show solution
Choose the correct answer
A voltmeter has an internal resistance
\[1000 Ω\] and can measure a potential difference of
\[0.05 V\]. A student wanted to extend the device's range to measure a potential difference
\[ 10 V\], so a series resistor was connected to increase the device's range.
The required resistance value for this purpose equals
\[ R_{es}=199000 \; Ω \;\;\;\;\;\; -C \] |
\[R_{es}=109000\; Ω \;\;\;\;\;\; -A \] |
\[R_{es} = 250000\; Ω \;\;\;\;\;\; -D \] |
\[R_{es} =165000\; Ω\;\;\;\;\;\; -B \] |
Click here to show the solution
Choose the correct answer
A capacitor with capacitance
\[20𝜇𝐹\] uncharged was connected in series with a resistor
\[150 Ω\] and a battery as shown in the figure below. The percentage of capacitor charge after a time of
\[3 ms\] equals
\[ 0.47 \;\;\;\;\;\;-C\] |
\[0. 75 \;\;\;\;\;\;-A\] |
\[ 0.82 \;\;\;\;\;\;-D\] |
\[0.63\;\;\;\;\;\;-B\] |
Click here to show the solution
Choose the correct answer
A capacitor with capacitance
\[6𝜇𝐹 \] uncharged was connected in series with two resistors
\[ R_1=90 Ω ,R_2=30 Ω \] and a battery with voltage
\[50V\]. The time required to complete 50% charging of the capacitor equals
\[t =4.45 ×10^{-5 } \;\;S\;\;\;\;\;\;-C\] |
\[t =9.35 ×10^{-5 } \;\;S\;\;\;\;\;\;-A\] |
\[t =2.18 ×10^{-5 } \;\;S\;\;\;\;\;\;-D\] |
\[t =6.86 ×10^{-5 } \;\;S\;\;\;\;\;\;-B\] |
Click here to show the solution
Choose the correct answer
A capacitor with capacitance
\[2𝜇𝐹\] was connected with two resistors
\[ R_1=500 Ω ,R_2=300 Ω \] and a battery until the charging process was completed as shown in the figure below. The time constant for completing the discharging process equals
\[𝜏=1.6×10^{-3} \;\;S\;\;\;\;\;\;-C\] |
\[𝜏=2.6×10^{-3} \;\;S\;\;\;\;\;\;-A\] |
\[𝜏=3.1×10^{-3} \;\;S\;\;\;\;\;\;-D\] |
\[𝜏=4.2×10^{-3} \;\;S\;\;\;\;\;\;-B\] |
Click here to show the solution
Choose the correct answer
An electrical circuit consists of four resistors with values as shown in the figure below. The current intensity passing through each resistor is:
\[I_1=0.35 A \;\;\;, \;\;\;I_2=0.35 A \;\;\;, \;\;\;I_3=0.7 A \;\;\;\;\;\;-C\] |
\[I_1=0.25 A \;\;\;, \;\;\;I_2=0.25 A \;\;\;, \;\;\;I_3=0.5 A \;\;\;\;\;\;-A\] |
\[I_1=0.2 A \;\;\;, \;\;\;I_2=0.2 A \;\;\;, \;\;\;I_3=0.4 A \;\;\;\;\;\;-D\] |
\[I_1=0.5 A \;\;\;, \;\;\;I_2=0.5 A \;\;\;, \;\;\;I_3=0.2 A \;\;\;\;\;\;-B\] |
Click here to show solutionChoose the correct answer
In the figure below, an electrical circuit is shown with resistors, batteries, current direction, and positive direction indicated. One of the equations correctly represents the equation of one of the loops in the circuit (Kirchhoff's second law):
\[2−2I_1−2I_2−4I_3=0\;\;\;\;\;\;-C\] |
\[6−I_1−2I_2=0 \;\;\;\;\;\;-A\] |
\[4−I_1+4I_3=0\;\;\;\;\;\;-D\] |
\[2−2I_1−2I_2−4I_3=0\;\;\;\;\;\;-B\] |
Click here to show solutionChoose the correct answer
In the circuit below, the potential difference between points A and B equals:
\[∆𝑉=11.44\;\;V \;\;\;\;\;\;-C\] |
\[∆𝑉=8.66\;\;V \;\;\;\;\;\;-A\] |
\[∆𝑉=5.42\;\;V \;\;\;\;\;\;-D\] |
\[∆𝑉=13.57\;\;V \;\;\;\;\;\;-B\] |
Click here to show solutionChoose the correct answer
A Wheatstone bridge was constructed using a copper wire of length 2m with a sliding contact point. Two resistors were placed on the other end: \[R_1=80 Ω , R_2=R\]. The contact point was moved until the galvanometer reading became zero at contact point C, which is 0.4 m from the end of the wire A. The value of \[R_2\] equals:
\[ R_2 = 10\; Ω \;\;\;\;\;\; -C \] |
\[R_2 = 20\; Ω \;\;\;\;\;\; -A \] |
\[R _2= 30\; Ω \;\;\;\;\;\; -D \] |
\[R_2 =40\; Ω\;\;\;\;\;\; -B \] |
Click here to show solutionChoose the correct answer
In the figure below, for loop 1 according to sign conventions and the assumed clockwise positive direction, one of the loop components has a negative voltage:
21 ohm resistor -C |
5V battery -A |
7V battery-D |
10 ohm resistor-B |
Click here to show solutionChoose the correct answer