Physics
📄 Print pdf
00971504825082
Light Reflection Fermat's Principle
Light reflection is the bouncing back of light when it hits a barrier
Light is a wave that reflects in the same medium (wave speed is constant)
And the source is the same for incident and reflected waves (frequency is constant)
Since wave speed and frequency are constant, therefore wavelength is constant
The incident ray represents number
\[.................\]
The reflected ray represents number
\[.................\]
The angle of incidence represents number
\[.................\]
The angle of reflection represents number
\[.................\]
The perpendicular to the surface represents number
\[.................\]
The reflecting surface represents number
\[.................\]
Question: What is the law of reflection?
In this simulation, the reflection of light on a reflective mirror surface is studied
Measure the angle of incidence and the angle of reflection
(Change the angle of the incident ray and take readings of the angle of incidence (the angle between the incident ray and the perpendicular to the surface)
and the angle of reflection (the angle between the reflected ray and the perpendicular to the surface)
Observe the incident ray, reflected ray, and the perpendicular to the surface
Through the experiment, complete the following table
Reflection Law Experiment
Fill in the following table, then click the "Check Answer" button to verify your answers and deduce the reflection law.
Reflection Angle \[𝜃_r\]
Incidence Angle \[𝜃_i\]
Attempt Number
Result
\[𝜃_r = \] degrees
\[𝜃_i = \] degrees
1
\[𝜃_r = \] degrees
\[𝜃_i = \] degrees
2
\[𝜃_r = \] degrees
\[𝜃_i = \] degrees
3
\[𝜃_r = \] degrees
\[𝜃_i = \] degrees
4
\[𝜃_r = \] degrees
\[𝜃_i = \] degrees
5
Conclusion:
After checking the answers, the reflection law conclusion will appear here.
1 Example
Light fell on a reflective surface as in the figure below, then the reflection angle equals
Choose the correct answer
A
𝜃₂ = 50°
B
𝜃₂ = 80°
C
𝜃₂ = 40°
D
𝜃₂ = 100°
2 Example
Two mirrors placed perpendicularly as in the figure below, light was incident on one of them with an incidence angle of 40°, then the angle at which light reflects on the second mirror equals
Choose the correct answer
A
𝜃 = 50°
B
𝜃 = 40°
C
𝜃 = 30°
D
𝜃 = 35°
Useful Information: Regular Reflection and Irregular Reflection
Regular reflection occurs on smooth surfaces
Regular reflection obeys the reflection law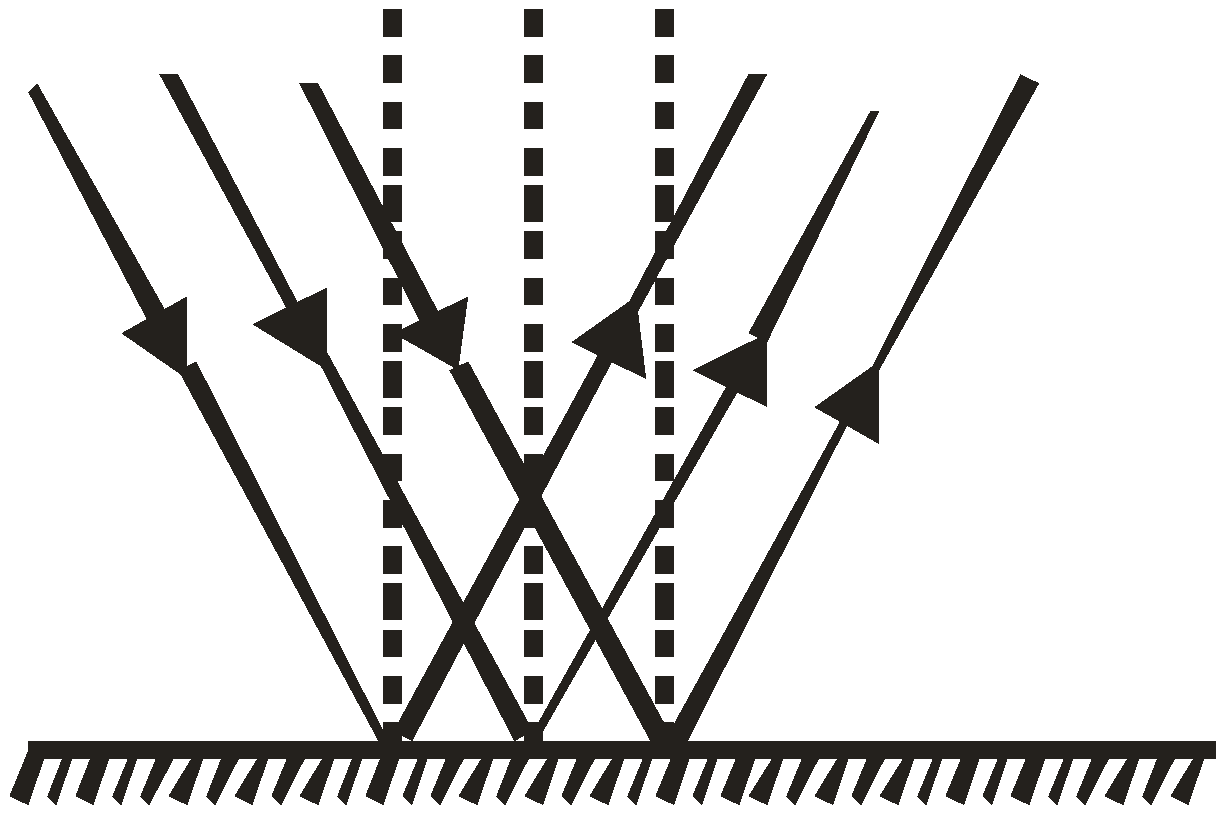 
Irregular reflection occurs on rough surfaces
Irregular reflection obeys the reflection law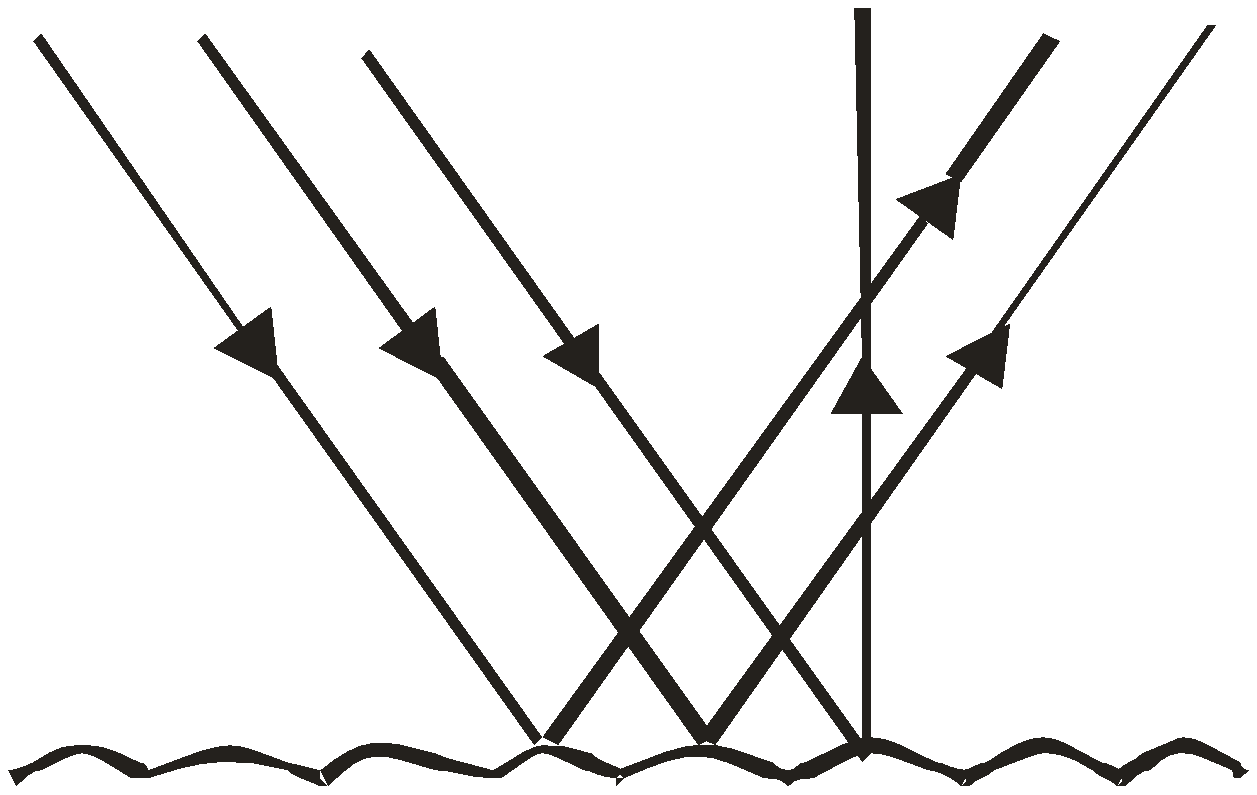 
The difference between regular and irregular reflection
In regular reflection, incidence angles are equal and equal to reflection angles, light reflects in one direction
In irregular reflection, incidence angles are not equal but each incidence angle equals its reflection angle, light reflects in all directions
Traffic signs with rough surfaces are used
so that light reflects on them and we can see them from all directions
Short Test: Light Reflection
Image Characteristics in Plane Mirrors
"Compare between object length and image length
Compare between object distance from mirror and image distance from mirror
Is the image upright or inverted
Is the image laterally inverted or upright
Is the image real or virtual
If the image results from the intersection of reflected rays, it is real
If the image results from the intersection of the extensions of reflected rays, it is virtual
Spherical Mirrors
"Spherical mirrors are part of a glass sphere
There are two types of them
Concave mirror: its inner surface is the reflective surface
Convex mirror: its outer surface is the reflective surface
Some Terms
Center of Curvature: is the center of the sphere from which the spherical mirror (convex or concave) is obtained. Denoted by the letter
( c)
The central point of the reflective surface of the spherical mirror is called the Pole. It lies on the mirror and is denoted by the letter
( p)
The straight line connecting the Pole and the Center of Curvature is called
(Principal Axis)
The point where reflected rays or their extensions meet if they fall parallel
(Focus F )
There is a relationship between the focal length (distance from focus to mirror f)
and the radius of curvature (distance from center of curvature to mirror R )
\[f=\dfrac{R}{2}\]
Images in Spherical Mirrors
First, we must know the path of rays in spherical mirrors
Light incident parallel to the principal axis reflects passing through the focus or its extension passes through the focus
Light incident passing through the focus or its extension passes through the focus reflects parallel to the principal axis
Light incident passing through the center of curvature reflects back on itself
All incident rays obey the reflection law
We will place the object in different positions and determine image characteristics
Spherical Mirrors Types and Properties Table
Spherical Mirrors Types and Properties
Select the correct answers from the dropdown lists, then click the "Check Answers" button to see your result.
Spherical Mirror Type
Object Position
Formed Image Characteristics
Concave
At Focus
Concave
Between Focus and Mirror
Concave
Between Focus and Center of Curvature
Concave
At Center of Curvature
Concave
Beyond Center of Curvature
Convex
Any Position
Score: 0/6
Click here to show solution method
Play and Learn
In this simulation, a dinosaur game is brought closer and farther from a plane, concave, and convex mirror, observe the image
Change the mirror type through the icon at the top left
f= 0 Plane mirror
f>0 Convex mirror
0>f Concave mirror
Through the previous experiment and the information you gained, answer the following questions
An object was placed in front of a mirror and no matter how the object distance from the mirror changed, the image remained upright, then the mirror is
An object was placed in front of a concave mirror at the center of curvature, then the image is
An object was placed in front of a concave mirror at the focus, then the image
An object was placed in front of a mirror and an image larger than the object appeared
Drawing Skill
Complete drawing the formed images when placing an object in front of a concave mirror in different positions and verify the solution by clicking the icons below the drawing
Object beyond center of curvature
Object at center of curvature
Object between focus and center of curvature
Object at focus
Object between focus and mirror pole
Useful Information: Spherical Mirrors Laws
Through triangle similarity, mirror equations are derived
\[\dfrac{1}{𝑥_o}+\dfrac{1}{𝑥_i}=\dfrac{1}{f}\]
There is a problem in applying the previous equation which is the signs for the previous values. The following table shows the signs
-
+
Sign
Convex mirror - Diverging
Concave mirror - Converging
\[f\] Focal Length
Placing an image for an object in front of a mirror
Placing an object in front of a mirror
\[X_0\]Object distance from mirror
Virtual image - Upright - Image behind mirror
Real image - Inverted - In front of mirror
\[X_I\]Image distance from mirror
We put signs only for known values
Magnification is the ratio between image length \[{h_i}\] to object length \[{h_o}\]
It equals negative image distance to object distance
\[M = \dfrac{h_i}{h_o} = -\dfrac{𝑥_i}{𝑥_o} \]
Note: magnification sign is always opposite to image distance sign
In this simulation, move the point above the object to change object distance and length. Move the focus position to change focal length. Move the circle below the object to the right side of the mirror to change it to a convex mirror
Change object position each time and determine focal length value and object distance from the experiment and calculate image distance and magnification each time
Calculate Spherical Mirror Properties
Usage Instructions:
1. Choose the spherical mirror type (concave or convex)
2. Enter the focal length \[(f)\] and object distance from mirror \[(Xo)\]
3. Try to calculate image distance \[(Xi)\] and magnification \[(m)\] yourself
4. Click the "Check Solutions" button to verify your answers
Mirror equation: 1\[\frac {1}{f} = \frac {1}{X_o }+\frac {1}{X_i}\] | Magnification equation:\[m =\frac {-X_i}{X_o}\]
Note: Focal length for concave mirror is positive, for convex mirror is negative
Spherical Mirror Type
Focal Length \[(f)\]
Object Distance from Mirror \[(Xo)\]
Image Distance from Mirror \[(Xi)\]
Magnification \[(m)\]
Spherical Mirrors Quick Quiz
🧮 Calculator
🗑️
✏️ قلم
Light Reflection Fermat's Principle |
Light is a wave that reflects in the same medium (wave speed is constant)
And the source is the same for incident and reflected waves (frequency is constant)
Since wave speed and frequency are constant, therefore wavelength is constant
The incident ray represents number \[.................\] The reflected ray represents number \[.................\] The angle of incidence represents number \[.................\] The angle of reflection represents number \[.................\] The perpendicular to the surface represents number \[.................\] The reflecting surface represents number \[.................\] Question: What is the law of reflection?
In this simulation, the reflection of light on a reflective mirror surface is studied
Measure the angle of incidence and the angle of reflection
(Change the angle of the incident ray and take readings of the angle of incidence (the angle between the incident ray and the perpendicular to the surface)
and the angle of reflection (the angle between the reflected ray and the perpendicular to the surface)
Observe the incident ray, reflected ray, and the perpendicular to the surface
Through the experiment, complete the following table
Reflection Law Experiment
Fill in the following table, then click the "Check Answer" button to verify your answers and deduce the reflection law.
Reflection Angle \[𝜃_r\] |
Incidence Angle \[𝜃_i\] |
Attempt Number |
Result |
\[𝜃_r = \] degrees |
\[𝜃_i = \] degrees |
1 |
|
\[𝜃_r = \] degrees |
\[𝜃_i = \] degrees |
2 |
|
\[𝜃_r = \] degrees |
\[𝜃_i = \] degrees |
3 |
|
\[𝜃_r = \] degrees |
\[𝜃_i = \] degrees |
4 |
|
\[𝜃_r = \] degrees |
\[𝜃_i = \] degrees |
5 |
Conclusion:
After checking the answers, the reflection law conclusion will appear here.
Light fell on a reflective surface as in the figure below, then the reflection angle equals
Choose the correct answer
Two mirrors placed perpendicularly as in the figure below, light was incident on one of them with an incidence angle of 40°, then the angle at which light reflects on the second mirror equals
Choose the correct answer
Useful Information: Regular Reflection and Irregular Reflection
Regular reflection obeys the reflection law Irregular reflection occurs on rough surfaces
Irregular reflection obeys the reflection law The difference between regular and irregular reflection
In regular reflection, incidence angles are equal and equal to reflection angles, light reflects in one direction
Is the image laterally inverted or upright
Is the image real or virtual If the image results from the intersection of the extensions of reflected rays, it is virtual \[f=\dfrac{R}{2}\]
Select the correct answers from the dropdown lists, then click the "Check Answers" button to see your result.
Through triangle similarity, mirror equations are derived
\[\dfrac{1}{𝑥_o}+\dfrac{1}{𝑥_i}=\dfrac{1}{f}\] There is a problem in applying the previous equation which is the signs for the previous values. The following table shows the signs
- + Sign Convex mirror - Diverging Concave mirror - Converging \[f\] Focal Length Placing an image for an object in front of a mirror Placing an object in front of a mirror \[X_0\]Object distance from mirror Virtual image - Upright - Image behind mirror Real image - Inverted - In front of mirror \[X_I\]Image distance from mirror We put signs only for known values
Magnification is the ratio between image length \[{h_i}\] to object length \[{h_o}\]
It equals negative image distance to object distance
\[M = \dfrac{h_i}{h_o} = -\dfrac{𝑥_i}{𝑥_o} \] Note: magnification sign is always opposite to image distance sign
1. Choose the spherical mirror type (concave or convex) 2. Enter the focal length \[(f)\] and object distance from mirror \[(Xo)\] 3. Try to calculate image distance \[(Xi)\] and magnification \[(m)\] yourself 4. Click the "Check Solutions" button to verify your answers Note: Focal length for concave mirror is positive, for convex mirror is negative
Image Characteristics in Plane Mirrors
"Compare between object length and image length
Compare between object distance from mirror and image distance from mirror
Is the image upright or inverted
If the image results from the intersection of reflected rays, it is real
Spherical Mirrors
There are two types of them
Concave mirror: its inner surface is the reflective surface
Convex mirror: its outer surface is the reflective surface
Center of Curvature: is the center of the sphere from which the spherical mirror (convex or concave) is obtained. Denoted by the letter
The central point of the reflective surface of the spherical mirror is called the Pole. It lies on the mirror and is denoted by the letter
( p)
The straight line connecting the Pole and the Center of Curvature is called
(Principal Axis)
The point where reflected rays or their extensions meet if they fall parallel
(Focus F )
There is a relationship between the focal length (distance from focus to mirror f)
and the radius of curvature (distance from center of curvature to mirror R )
Images in Spherical Mirrors
First, we must know the path of rays in spherical mirrors
Light incident parallel to the principal axis reflects passing through the focus or its extension passes through the focus
Light incident passing through the focus or its extension passes through the focus reflects parallel to the principal axis
Light incident passing through the center of curvature reflects back on itself
All incident rays obey the reflection law
We will place the object in different positions and determine image characteristics
Spherical Mirrors Types and Properties Table
Spherical Mirrors Types and Properties
Spherical Mirror Type
Object Position
Formed Image Characteristics
Concave
At Focus
Concave
Between Focus and Mirror
Concave
Between Focus and Center of Curvature
Concave
At Center of Curvature
Concave
Beyond Center of Curvature
Convex
Any Position
Click here to show solution method
Play and Learn
In this simulation, a dinosaur game is brought closer and farther from a plane, concave, and convex mirror, observe the image
Change the mirror type through the icon at the top left
f= 0 Plane mirror
f>0 Convex mirror
0>f Concave mirror
Drawing Skill
Complete drawing the formed images when placing an object in front of a concave mirror in different positions and verify the solution by clicking the icons below the drawing
Object beyond center of curvature
Object at center of curvature
Object between focus and center of curvature
Object at focus
Object between focus and mirror pole
In this simulation, move the point above the object to change object distance and length. Move the focus position to change focal length. Move the circle below the object to the right side of the mirror to change it to a convex mirror
Change object position each time and determine focal length value and object distance from the experiment and calculate image distance and magnification each time
Calculate Spherical Mirror Properties
Usage Instructions:
Spherical Mirror Type
Focal Length \[(f)\]
Object Distance from Mirror \[(Xo)\]
Image Distance from Mirror \[(Xi)\]
Magnification \[(m)\]
No comments:
Post a Comment